Cho ΔABC có BD là tia phân giác của góc B. CE là tia phân giác của góc C
a, CMR : ΔAED cân tại A
Cho tam giác ABC cân tại A, góc A tù, BD, CE lần lượt là tia phân giác của góc B,C. BH, CK lần lượt vuông góc với CE, BD tại H,K. - ED//BC - Gọi I là giao điểm của BD và CE, chứng minh AI là tia phân giác của góc A - BH=CK - Vẽ các tia Bx vuông góc với BD, Cy vuông góc với CE. Bx và Cy cắt nhau tại F, chứng minh A,F,I thẳng hàng
1. Cho x'x//y'y, MN cắt x'x tại M, y'y tại N. E, F thuộc y'y về 2 phía của N : NE =NF=MN.CMR:a) ME, MF là 2 tia phân giác của góc xMN, x'MN b) tam giác MEF vuông
2. Cho tam giác ABC cân tại A, trên tia đối của tia BC lấy điểm D ,E sao cho CE=BD . Nối AD, AE. So sánh góc ABD với ACE. CM tam giác ADE cân
3. CHOtam giác ABC tia phân giác góc B, C cắt nhau tại O. Qua O kẻ đường thẳng song song với BC, cắt AB tại D, cắt AC tại E. CM DE =DB +EC
4. CHO TAM GIÁC ABC VUÔNG TẠI A và góc B =60°. Cx vuông góc với BC, trên tia Cx lấy đoạn CE=CA ( CE, CA CÙNG PHÍA VỚI BC ). KÉO DÀI CB LẤY F : BF =BA. CM TAM GIÁC ABC ĐỀU VÀ 3 ĐIỂM E, A, F THẲNG HÀNG
5. Cho tam giác ABD : góc B=2D, kẻ AH vuông góc với BD (H thuộc BD ). Trên tia đối của tia BA lấy BE =BH. Đường thẳng EH cắt AD tại F. CM FH=FA =FD
6. Cho tam giác ABC cân tại A, đường cao AH. Trên tia AH lấy điểm D sao cho H là trung điểm của đoạn thẳng AD. Nối CD. CM CD=AB và CB là tia phân giác của góc ACD
7. CHO tam giác ABC cân tại A, đường cao BH. CMR góc BAC =2 CBH
8. Cho tam giác ABC có góc B =60, 2 tia phân giác AD và CE của tam giác cắt nhau tại I. CMR tam giác IDE cân
9. Cho tam giác ABC cân tại A, đường cao AH, HD, HE lần lượt là đường cao của tam giác AHB, AHC. trên tia đối của tia DH, EH lấy điểm M, N: DM=DB, EN =EH.CMR: a) tam giác AMN và tam giác HMN cân b) góc MAN=2BAC
Cho tam giác abc cân tại a. kẻ bd vuông góc với ac, ce vuông góc ab. Gọi i là giao điểm bd và ce. Cmr:
a) be = cd b) ai là tia phân giác .của góc bac
Cho tam giác ABC có AB=AC,BC<AB, gọi M là trung điểm của BC.
a,CMR: tam giác ABM=ACM. Từ đó suy ra AM là tia phân giác của góc BAC
b,Trên cạnh AB lấy D sao cho B=CD. Kẻ tia phân giác của góc BCD,tia nay cắt BD tại N.CMR: CN vuông góc với BD
c,Trên tia đối CA lấy E sao cho CE=AD . CMR : góc BCE=ADC
d, CMR: BA=BE
Bài 1: Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và // với BC cắt AC ở E. Đường thẳng qua E và // với AB cắt BC ở F. CMR:
a) AD = EF
b) Tam giác ADE = tam giác EFC
Bài 2: Cho tam giác ABC, tia phân giác của góc C cắt AB ở D. Trên tia đối của tia CA lấy điểm E sao cho CE = CB.
a) CM CD//EB
b) Tia phân giác của góc E cắt đường thẳng CD tại F. Vẽ CK vuông góc với EF tại K. CM CK là tia phân giác của góc ECF
Bài 3: Cho tam giác ABC cân tại A, trên tia AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE=BD, DE cắt BC tại I. Trên tia đối của tia BC lấy điểm F sao cho BF=CI. CMR:
a) Tam giác BFD = tam giác CIE
b) Tam giác DFI cân
c) I là trung điểm của DE
giúp mình với nhé!
cho tam giác ABC : A = 90: Vẽ N thuộc BC sao cho BN = BA. Vẽ BD vuông góc AN ( D thuộc AN )
a, CMR: BD là tia phân giác của ABC
b, Lấy M thuộc CB sao cho CM = CA. Kẻ tia CE là tia pphângiacs ACN. CMR: ME vuông góc AN.
c, Cho CE, BD cắt nhau tại O, cắt AM tại F, BD cắt AM tại I. CM: IE = AD.
có vẽ hình
a: Xét ΔBDA vuông tại D và ΔBDN vuông tại D có
BA=BN
BD chung
Do đó: ΔBDA=ΔBDN
=>\(\widehat{ABD}=\widehat{NBD}\)
=>\(\widehat{ABD}=\widehat{CBD}\)
=>BD là phân giác của góc ABC
cho tam giác ABC cân tại A kẻ BD vuông góc với AC . CE vuông góc với AB. Gọi k là giao điểm của BD và CE. CMR
a. AK là tia phân giác của góc A
b. CM AK vuông góc với BC
Cho tam giác ABC cân tại A. Kẻ các tia phân giác BD, CE. Lấy M là trung điểm của BC.
a) Chứng minh AM là tia phân giác của góc BAC.
b) Ba đường thẳng AM, BD, CE đồng quy tại H.
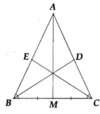
a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.
1.cho góc nhọn xOy , lấy điểm A thuộc Ox, B thuộc Oy sao cho OA=OB, kẻ AH vuông góc với Oy, BK vuông Ox
Chứng minh tam giác OHK cân
Gọi I là giao diểm của AH và BK. Chứng minh OI là tia phân giác của xOy
2. Cho tam giác ABC có B=60 độ, phân giác BD, từ A kẻ Ax // BC cắt tia DB tại E
Chứng minh rằng ABE cân
Tính góc BAE
3. Cho tam giác ABC tia phân giác của góc C cắt AB ở D. Trên tia đối của CA lấy E sao cho CE=CD
Chứng minh CD//EB
Tia phân giác của góc E cắt đường thẳng CD tại F, vẽ CK vuông góc EF tại K. Chứng minh CK là tia phân giác của góc ECF
4. Cho tam giác ABC cân tại A, trên AB lấy D, trên tia đối của tia CA lấy E sao cho CE=BD, DE cắt BC tại I. Trên tia đối của tia CA lấy E sao cho CE=BD, DE cắt BC tại I. Trên tia đối của tia BC lấy F sao cho BF= CI. Chứng minh rằng
Tam giác BFD=CIE
Tam giác DFI cân
I là trung diểm của DE
a) Xét Tàm giác vuông OBK và Tam giác vuông OAH có :
OA = OB (GT)
<O chung
=> Tam giác vuông OBK = Tam giác vuông OAH ( cạnh góc vuông - góc nhọn kề )
=> OH = OK (2CTU)
Xét Tam giác OHK có :
OH = OK
=> Tam giác OHK cân tại O (dpcm)
b) Vì Tam giác OBK và Tam giác OAH (cmt)
=> <OKB = <OHA (2GTU)
TC : OH = OK (cmt)
OA = OB (GT)
mà OH = OB + BH
OK = OA + AK
=> AK = BH
Xét Tam giác vuông AIK và Tam giác vuông BIH
AK = BH
<OKB = <OHA
=> Tam giác vuông AIK = Tam giác vuông BIH ( cạnh góc vuông - góc nhọn kề)
=> AI = BI (2CTU)
Xét Tam giác OAI = Tam giác OBI có :
OA = OB (GT)
OI chung
AI = BI (cmt)
=> Tam giác OAI = Tam giác OBI (c.c.c)
=> <AOI = <BOI (2GTU)
=> OI là tia phân giác của <xOy (dpcm)