Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới) là tam giác vuông cân.

Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới) là tam giác vuông cân
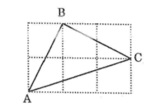
Đặt độ dài cạnh ô vuông là 1 (đơn vị chiều dài)
Áp dụng định lí pitago ta có:
AB2=12+22=1+4=5
BC2=12+22=1+4=5
AC2=32+12=9+1=10
Suy ra: AC2=AB2+BC2
Áp dụng định lí pitago đảo ta có tam giác ABC vuông tại B
Lại có: AB2=BC2=5 suy ra: AB = BC. Do đó, tam giác ABC là tam giác cân tại B.
Vậy tam giác ABC vuông cân tại B
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới ) là tam giác nhọn.
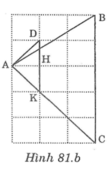
Nối A với D tạo thành đường chéo ô vuông
Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ngang ô vuông đi qua A. ( như hình vẽ)
Ta có: ΔAHK vuông cân tại H =>∠HAK =45o
ΔAHD vuông cân tại H=>∠HAD =45o
=>∠DAK =∠HAK +∠HAD =45o+45o=90o
hay ∠DAC =90o
=>∠BAC <90o
Hình vuông có 4 góc, mỗi góc bằng 900. Từ hình vẽ suy ra: ∠ACB <90o và ∠ABC <90o
Vậy tam giác ABC là tam giác nhọn

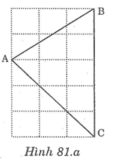
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông là tam giác giác vuông cân (h.67) ?
Gọi độ dài cạnh của mỗi ô vuông là 1.
Theo định lí Py-ta-go:
AB2 = 12 + 22 = 1 + 4 = 5
BC2 = 12 + 22 = 1 + 4 = 5
AC2 = 12 + 32 = 1 + 9 = 10
Do AB2 = BC2 nên AB = BC
Do AB2 + BC2 = AC2 nên \(\widehat{ABC}=90^o\)
Vậy \(\Delta ABC\) vuông cân tại B.
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông như hình 61 là tam giác nhọn ( tức là tam giác có cả ba góc đều là góc nhọn )
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (h.62) là tam giác nhọn ?
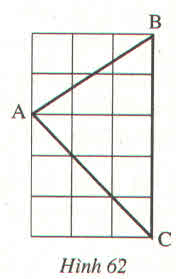
Giả sử độ dài mỗi ô vuông nhỏ là 1
Đường chéo mỗi ô vuông là Căn 2.
Độ dài các cạnh AB, AC, BC lần lượt là: ( căn 13) , 3 căn 2, 5
Ta thấy 3 cạnh không bằng nhau nên không phải tam giác đều.
Thử định lý pytago đảo không đúng nên không phải tam giác vuông.
So sánh tỉ lện giữ cách cạnh đều nhỏ hơn 2. Nên trong tam giác không có góc tù. Vậy tam giác là tam giác nhọn
Cho tam giác ABC vuông cân tại A. Trên nửa mặt phẳng bờ BC không chứa A vẽ tam giác BCD vuông cân tại B.
a) Chứng minh rằng tứ giác ABDC là hình thang vuông.
b) Trên cạnh AB lấy điểm M. Kẻ tia Mx vuông góc với MC tại M. Tia Mx cắt BD tại N. Chứng minh tam giác MCN vuông cân.
Cho tam giác ABC vuông cân tại A. Trên nửa mặt phẳng bờ BC không chứa A vẽ tam giác BCD vuông cân tại B.
a) Chứng minh rằng tứ giác ABDC là hình thang vuông.
b) Trên cạnh AB lấy điểm M. Kẻ tia Mx vuông góc với MC tại M. Tia Mx cắt BD tại N. Chứng minh tam giác MCN vuông cân.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng tứ giác BDEC là hình thang cân.
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng AECB là hình thang vuông
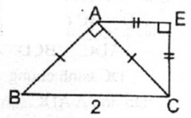
Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông