Cho 2 đường tròn (O) và (O') tiếp xúc ngoài tại A. Một đường thẳng d qua A cắt (O) và (O') lần lượt tại E và F. Tìm tập hợp trung điểm M của đoạn EF khi d quay quanh điểm A.

Những câu hỏi liên quan
Cho (O) và điểm A nằm ngoài đường tròn. Kẻ dây BC bất kì đi qua A
a, Xác định tâm D của đường tròn đi qua điểm A và tiếp xúc với (O) tại B.
Xác định tâm E của đường tròn đi qua điểm A và tiếp xúc với (O) tại C.
b, CMR DE luôn đi qua một điểm cố định khi dây BC quay quanh điểm A. Tìm tập hợp các điểm M là giao điểm thứ 2 của (D) và (E)
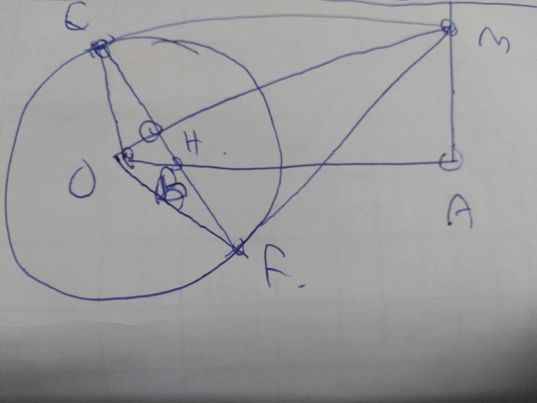
Cho đường tròn (O;R) và điểm A năm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E, F là tiếp điểm). EF cắt OM và OA lần lượt tại H và Ka, Chứng minh: H là trung điểm EFb, Chứng minh: O,M,A,F cùng thuộc 1 đường trònc, Chứng minh:OK.OA R2d, Xác định vị trí điểm M trên đường thẳng d để tam giác OHK có diện tích lớn nhấto l m . v n
Đọc tiếp
Cho đường tròn (O;R) và điểm A năm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E, F là tiếp điểm). EF cắt OM và OA lần lượt tại H và K
a, Chứng minh: H là trung điểm EF
b, Chứng minh: O,M,A,F cùng thuộc 1 đường tròn
c, Chứng minh:OK.OA = R2
d, Xác định vị trí điểm M trên đường thẳng d để tam giác OHK có diện tích lớn nhất
o l m . v n
Cho đường tròn (O;R) và điểm A cố định ở ngoài đường tròn . Vẽ đường thẳng d vuông góc với OA tại A . Trên d lấy điểm M . Qua M kẻ 2 tiếp tuyến ME,MF tới đường tròn (O;R) tiếp điểm lần lượt là E và F . Nối EF cắt OM tại H,cắt OA tại Ba) Chứng minh OM vuông góc với EFb) Cho biết R`6` cm,OM`10` cm . Tính OHc) Chứng minh 4 điểm A,B,H,M cùng thuộc một đường tròn
Đọc tiếp
Cho đường tròn (O;R) và điểm A cố định ở ngoài đường tròn . Vẽ đường thẳng d vuông góc với OA tại A . Trên d lấy điểm M . Qua M kẻ 2 tiếp tuyến ME,MF tới đường tròn (O;R) tiếp điểm lần lượt là E và F . Nối EF cắt OM tại H,cắt OA tại B
a) Chứng minh OM vuông góc với EF
b) Cho biết R`=6` cm,OM`=10` cm . Tính OH
c) Chứng minh 4 điểm A,B,H,M cùng thuộc một đường tròn
a:Xét (O) có
MF,ME là tiếp tuyến
Do đó: MF=ME
=>M nằm trên đường trung trực của FE(1)
OE=OF
=>O nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra OM là đường trung trực của EF
=>OM\(\perp\)EF tại H và H là trung điểm của EF
b: ΔOMF vuông tại F
=>\(FO^2+FM^2=OM^2\)
=>\(FM^2=10^2-6^2=64\)
=>\(FM=\sqrt{64}=8\left(cm\right)\)
Xét ΔOFM vuông tại F có FH là đường cao
nên \(OH\cdot OM=OF^2\)
\(\Leftrightarrow OH\cdot10=6^2=36\)
=>OH=36/10=3,6(cm)
c: Xét tứ giác BHMA có
\(\widehat{BHM}+\widehat{BAM}=90^0+90^0=180^0\)
=>BHMA là tứ giác nội tiếp
=>B,H,M,A cùng thuộc một đường tròn
Đúng 2
Bình luận (0)
Cho đường tròn (O;R) và điểm A cố định ở ngoài đường tròn . Vẽ đường thẳng d vuông góc với OA tại A . Trên d lấy điểm M . Qua M kẻ 2 tiếp tuyến ME,MF tới đường tròn (O;R) tiếp điểm lần lượt là E và F . Nối EF cắt OM tại H,cắt OA tại B
* Yêu cầu vẽ hình
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Đọc tiếp
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Cho đường tròn tâm O bán kính R và điểm A nằm ngoài đường tròn sao cho Oa=2R. Đường thẳng d qua A cắt đường tròn tại E, f. Các tiếp tuyến tại E, F cắt nhau tại K. cmr: khi d quay quanh A thì K chạy trên một đường thẳng cố định
Cho đường tròn(O,R) từ điểm A nằm ngoài đường tròn vẽ 2 tiếp tuyến AB, AC của (O) ( B, C là tiếp điểm) và cát tuyến AE. Qua E vẽ tiếp tuyến thứ 3 cắt AB, ÂC lần lượt tại P,Q. Gọi I là trung điểm của EF
a, CM: A,B,O,I,C cùng nằm trên một đường tròn.
b, CM chu vi tam giác APQ không đổi khi AEF quay quanh A
c,OI cắt đường thẳng PQ tại S. CM: SF là tiếp tuyến của (O)
Cho đường tròn (O:R) và điểm E nằm ngoài đường tròn sao cho EO=2R. Đường thẳng EO cắt đường tròn tại A và B. Kẻ 2 tiếp tuyến Ax và By của đường tròn O và tiếp tuyến thứ 3 qua E tiếp xúc với đường tròn (O) tại M cắt Ax,By lần lượt tại C và D. Tính CD theo R
Cho đường tròn (O;R) và điểm A năm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E, F là tiếp điểm). EF cắt OM và OA lần lượt tại H và Ka, Chứng minh: H là trung điểm EFb, Chứng minh: O,M,A,F cùng thuộc 1 đường trònc, Chứng minh:OK.OA ^{R^2}d, Xác định vị trí điểm M trên đường thẳng d để tam giác OHK có diện tích lớn nhất
Đọc tiếp
Cho đường tròn (O;R) và điểm A năm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E, F là tiếp điểm). EF cắt OM và OA lần lượt tại H và K
a, Chứng minh: H là trung điểm EF
b, Chứng minh: O,M,A,F cùng thuộc 1 đường tròn
c, Chứng minh:OK.OA = \(^{R^2}\)
d, Xác định vị trí điểm M trên đường thẳng d để tam giác OHK có diện tích lớn nhất