Tìm hai số tự nhiên abcd và bcd biết: abcd + bcd = 9192

Những câu hỏi liên quan
tìm hai số tự nhiên biết /abcd va /bcd biet
/abcd+/bcd=3186
Tìm hai số tự nhiên abcd và bcd biết
abcd + bcd =3186
Theo đề ra ta có :
abcd + bcd = 3186
a x 1000 + bcd + bcd = 3186
a x 1000 + bcd x 2 = 3186
=> a = 2 ; bcd = 593
Vậy abcd = 2593 và bcd = 593
Đúng 0
Bình luận (0)
a, b, c, d là chữ số
a000 + bcd + bcd = 3186
2 x abcd = 3186 - a000 => 0 < a \(\le\)3
a = 1 thì bcd = (3186 - 1000) : 2 = 1092 (loại vì bcd có chữ số)
a = 2 thì bcd = (3186 - 2000) : 2 = 593
a = 3 thì bcd = (3186 - 3000) : 2 = 93 (loại vì bcd có 3 chữ số)
Vậy abcd = 2593 và bcd = 593
Đúng 0
Bình luận (0)
Tìm hai số tư nhiên abcd và bcd biết :
abcd + bcd = 3186
ta có:abcd+bcd=3186
ax1000+bcd+bcd=3186
ax1000+bcdx2=3186
a=3 và 3x1000=3000
3186-3000=186
bcd=186:2=93(sai)
a=2 và 2x1000=2000
3186-2000=1186
bcd=1186:2=593
abcd=2593
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
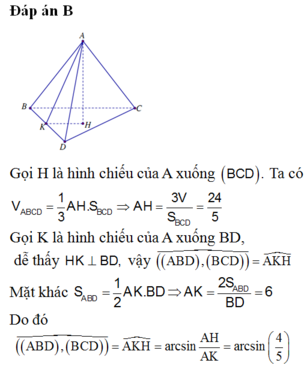
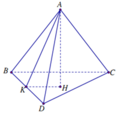
Cho tứ diện ABCD có BD 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD). A. arccos(4/15) B. 1 C. arcsin(4/5) D. arccos(4/5)
Đọc tiếp
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
A. arccos(4/15)
B. 1
C. arcsin(4/5)
D. arccos(4/5)
Cho tứ diện ABCD có BD 3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là A.
a
r
c
sin
33
40
B.
a
r
c...
Đọc tiếp
Cho tứ diện ABCD có BD =3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là
A. a r c sin 33 40
B. a r c sin 11 40
C. a r c cos 33 40
D. a r c cos 11 40
Chọn A.
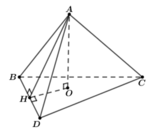
Gọi O là chân đường vuông góc kẻ từ A đến mặt phẳng (BCD)
![]()
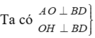
![]()
![]()
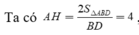
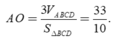
Khi đó ta tính được
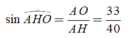
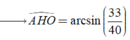
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có BD2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng 16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD).
Đọc tiếp
Cho tứ diện ABCD có BD=2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng 16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD).
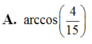

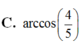
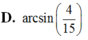
Cho tứ diện ABCD có BD2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD). A.
arccos
4
15
B.
arcsin
4
5
C.
arccos
4
5
D.
arcsin...
Đọc tiếp
Cho tứ diện ABCD có BD=2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD).
A. arccos 4 15
B. arcsin 4 5
C. arccos 4 5
D. arcsin 4 15
Tìm số tự thiên nhiên a,b,c,d biết:
\(\text{31(abcd + ab + ad + cd + 1) = 40 (bcd + b + d )}\)
Cho tứ diện ABCD. I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Xác định giao tuyến của hai mặt phẳng (GID) và (BCD). Tìm thiết diện của mặt phẳng (GIJ) với hình chóp ABCD. Thiết diện là hình gì