cho m=a,bcd n=a,bcd biết mn=230,213 tính m n
các bạn giúp mình với nhé cảm ơn
Những câu hỏi liên quan
Cho M =abc,d ; a,bcd.Biết M+N=203,313.Tính M-N
Giúp mình nhé mấy bạn!
M ; 100 phần
N : 1 phần
số M là :
203,313 : (100 + 1) x 100 = 201,3
số N là:
203,313 - 201,3 = 2,013
M - N là:
201,3 - 2,013 = 199,287
Đúng 0
Bình luận (0)
M ; 100 phần
N : 1 phần
số M là :
203,313 : (100 + 1) x 100 = 201,3
số N là:
203,313 - 201,3 = 2,013
M - N là:
201,3 - 2,013 = 199,287
Đúng 0
Bình luận (0)
M ; 100 phần
N : 1 phần
số M là :
203,313 : (100 + 1) x 100 = 201,3
số N là:
203,313 - 201,3 = 2,013
M - N là:
201,3 - 2,013 = 199,287
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tứ diện ABCD. Trên AB,AC lấy 2 điểm M,N sao cho MN không song song BC. Gọi O là một điểm nằm trong tam giác BCD. a) Tìm giao tuyến (OMN) và (BCD) b) Tìm giao điểm DB,DC, DA với (OMN) Vẽ hình giúp luôn ạ. Em cảm ơn
a: Trong mp(ABC), gọi E là giao điểm của MN và BC
\(O\in\left(OMN\right);O\in\left(BCD\right)\)
=>\(O\in\left(OMN\right)\cap\left(BCD\right)\)
\(E\in MN\subset\left(OMN\right);E\in BC\subset\left(BCD\right)\)
=>\(E\in\left(OMN\right)\cap\left(BCD\right)\)
Do đó: \(\left(OMN\right)\cap\left(BCD\right)=OE\)
b: Chọn mp(BCD) có chứa DB
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi F là giao của OE với DB
=>F là giao của DB với mp(OMN)
Chọn mp(BCD) có chứa DC
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi K là giao của OE với DC
=>K là giao của DC với mp(OMN)
Đúng 2
Bình luận (1)
Cho M = abc,d , N = a,bcd .Biết M+N + 203,313. Tính M-N (nhờ các bạn giải chi tiết giúp mình)
abc,d+a,bcd=203,313
101.a,bcd=203,313
a,bcd=2,013
Vậy M-N=201,3-2,013=199,287
Đúng 0
Bình luận (0)
ai tick cho mik đến 260 thì mik tick cho cả đời
Đúng 0
Bình luận (0)
Tìm các chữ số : a, b,c , d biết: a x bcd x bcd = abcabc. Mình sẽ tích cho bạn nào có câu trả lời đúng và nhanh nhất. Cảm ơn nhiệt tình.
Mọi người giúp mình giải bài này với ạ ! Mình cảm ơn :
Cho 2 hình chữ nhật ABCD và BCEF, BD = 15 m, AE = 20 m, BD vuông góc AE.
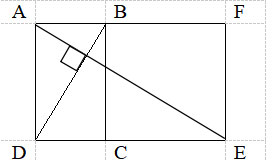
a) Tính diện tích tứ giác ABED.
b) Biết rằng CE = 2 x CD, tính diện tích của tam giác BCD và tam giác BCE.
Diện tích tam giác BCD là:
Đúng 2
Bình luận (1)
cứu mình với mình ko biết làm bài này với lại mình đang cần gấp giúp mình giải chi tiết nhé mình cảm ơn nhìu lắm lun ế .Cho tam giác ABC, trên BC lấy điểm chính giữa M .Nối A với M.Trên am lấy điểm N sao cho MN 1/3 x AM.Nối B với N cắt AC tại D.a.Kể tên các hình tam giác có trong hình vẽ .b.Diện tích hình tam giác MBN bằng 5 cm2.Tính diện tích hình tam giác ABM và diện tích hình tam giác ABC( Các bạn ơi có vẽ hình nhưng mình ko biết vẽ nhớ vẽ giúp mình nhớ mình đội ơn nhìu ) mình cảm ơn cảm ơn n...
Đọc tiếp
cứu mình với mình ko biết làm bài này với lại mình đang cần gấp giúp mình giải chi tiết nhé mình cảm ơn nhìu lắm lun ế .
Cho tam giác ABC, trên BC lấy điểm chính giữa M .Nối A với M.Trên am lấy điểm N sao cho MN =1/3 x AM.Nối B với N cắt AC tại D.
a.Kể tên các hình tam giác có trong hình vẽ .
b.Diện tích hình tam giác MBN bằng 5 cm2.Tính diện tích hình tam giác ABM và diện tích hình tam giác ABC
( Các bạn ơi có vẽ hình nhưng mình ko biết vẽ nhớ vẽ giúp mình nhớ mình đội ơn nhìu ) mình cảm ơn cảm ơn nhìu! giúp mình giải nhanh nhé !
Làm ơn giúp mình bài này với. Cảm ơn nhiều!
* Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung diểm của BD. Tính số đo góc BCD.
Cho tứ giác ABCD. Gọi M,N theo thứ tự là trung điểm của AB và CD và I là trung điểm của MN. G là trọng tâm tam giác BCD. Chứng minh A,I,G thẳng hàng. (Các bạn vẽ bhinhf giúp mình với)
Cho tứ diện ABCD có M, N, P lần lượt là trung tâm tam giác ABC, ACD, ABD
a) Chứng minh (BCD) song song các đường thẳng MN, MP, NP
b) Tìm thiết diện của tứ diện khi cắt bởi (MNP)
Giúp em với em cần gấp cảm ơn
Giải đơn giản và chu tiết
a/
Ta có
M là trọng tâm tg ABC \(\Rightarrow\dfrac{MI}{MA}=\dfrac{1}{2}\)
N là trọng tâm tg ACD \(\Rightarrow\dfrac{NK}{NA}=\dfrac{1}{2}\)
Xét tg AIK có
\(\dfrac{MI}{MA}=\dfrac{NK}{NA}=\dfrac{1}{2}\) => MN//IK (Talet đảo trong tam giác)
Ta có
\(I\in BC;BC\in\left(BCD\right)\Rightarrow I\in\left(BCD\right)\)
\(K\in CD;CD\in\left(BCD\right)\Rightarrow K\in\left(BCD\right)\)
\(\Rightarrow IK\in\left(BCD\right)\) Mà MN//IK (cmt) => MN//(BCD)
Các trường hợp khác c/m tương tự
b/
Trong (ABC) từ M dưng đường thẳng // BC cắt AB; AC tại X và Y
Trong (ACD) nối YN cắt AD tại Z
Xét tg ABC có
\(\dfrac{XB}{XA}=\dfrac{YC}{YA}=\dfrac{MI}{MA}=\dfrac{1}{2}\) (Talet trong tam giác)
XY//BC; \(BC\in\left(BCD\right)\) => XY//(BCD)
Xét tg ACK có
\(\dfrac{YC}{YA}=\dfrac{NK}{NA}=\dfrac{1}{2}\) => YN//CK => YZ//CD
mà \(CD\in\left(BCD\right)\) => YZ//(BCD)
=> (XYZ)//(BCD)
Ta có MP//(BCD); MN//(BCD) => (MNP)//(BCD)
mà \(M\in\left(MNP\right);M\in\left(XYZ\right)\)
\(\Rightarrow\left(MNP\right)\equiv\left(XYZ\right)\) (Từ 1 điểm ngoài 1 mặt phẳng cho trước chỉ có duy nhất 1 mặt phẳng đi qua điểm đã cho và // với mặt phẳng cho trước)
=> (XYZ) là thiết diện của tứ diện ABCD khi cắt bởi (MNP)
Đúng 0
Bình luận (0)