Cho hình bình hành ABCD có diện tích 1. Gọi M là trung điểm của cạnh BC; AM cắt đường chéo BD ở Q.
Tính diện tích tứ giác MQDC.
Cho hình bình hành ABCD M là trung điểm của cạnh BC biết diện tích hình tam giác IDM bằng 18 cm vuông tính diện tích hình bình hành ABCD
1.Hình thang ABCD có đáy lớn hơn đáy bé 3 dm. Hình bình hành ABMD có diện tích là 5 dm vuông. Tính diện tích hình thang ABCD ? ( chiều cao là 2,5 dm).
2. Cho htg ABC. Gọi M là trung điểm của cạnh BC, gọi N là trung điểm của cạnh AB. Biết diện tích htg ANM bằng 6cm vuông. Tính diện tích htg ABC ?
(2 bài này ở trang 7,8 vở toán nâng cao tập2 nha)
Ai nhanh mk tick3, kết bạn.
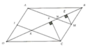
Cho hình bình hành ABCD có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME ^ BD tại E, CF ^ BD tại F.
Có B N = 1 3 B D , E M = 1 2 C F S B M N = 1 2 E M . B N = 1 2 . 1 2 C F . 1 3 B D = 1 6 S B C D = 1 12 S ⇒ S M N D C = 1 2 S − 1 12 S = 5 12 S
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích hình bình hành ABCD, diện tích tam giác ADM
A. S A B C D = 12 c m 2 ; S A D M = 3 c m 2
B. S A B C D = 12 c m 2 ; S A D M = 6 c m 2
C. S A B C D = 24 c m 2 ; S A D M = 3 c m 2
D. S A B C D = 24 c m 2 ; S A D M = 6 c m 2
SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A
Cho hình bình hành ABCD. Gọi M là trung điểm cạnh AD. CM cắt đường chéo BD tại E. Tính diện tích hình bình hành ABCD biết tam giác DME có diện tích 1m2
Dễ thấy SABCD = 2SADC (1)
Gọi O là giao điểm của AC và BD thì O là trung điểm của AC.
Tam giác ADC và tam giác CMD có chung đường cao kẻ từ C nên cho ta :\(\frac{S_{ADC}}{S_{CMD}}=\frac{AD}{MD}=2\)hay SADC = 2SCMD (2)
Tương tự : \(\frac{S_{CMD}}{S_{DME}}=\frac{CM}{ME}=3\)( vì E là trọng tâm của tam giác ADC ) hay SCMD = 3SDME (3)
Từ (1) (2) (3) suy ra SABCD = 12SDME = 12 m2
Cho hình bình hành ABCD. Gọi E,F,G,K lần lượt là trung điểm của cạnh AB,BC,CD,DA. Tính diện tích đa giác là phần chung của tứ giác AGCF,BGDK,CEAK,DEBF theo diện tích của hình bình hành ABCD. ( Theo ứng dụng của tỉ số diện tích trong tam giác)
Cho hình bình hành ABCD có diện tích là 1 cm. Gọi M là trung điểm BC. AM giao đường chéo BD ở Q. Tính diện tích tứ giác MQDC
Cho hình bình hành abcd có diện tích bằng 1. gọi m là trung điểm của bc, am cắt bd ở q. tính diện tích mqdc?
giải chi tiết giùm em với
Gọi O là giao điểm AC, BD=> O là trung điểm BC
=> Q là trọng tâm tam giác ABC \(\Rightarrow BQ=\frac{2}{3}BO=\frac{1}{3}BD\)
Lần lượt kẻ QK và OH vuông góc BC \(\Rightarrow\frac{QK}{OH}=\frac{BQ}{BO}=\frac{2}{3}\)(định lí Ta-lét)
Ta có: \(S_{BQM}=\frac{1}{2}.QK.BM\)
\(S_{OBC}=\frac{1}{2}.OH.BC=\frac{1}{2}.\left(\frac{3}{2}QK\right).2BM=3\left(\frac{1}{2}QK.BM\right)=3S_{BQM}\)
Lại có:\(S_{OBC}=\frac{1}{2}S_{BCD}=\frac{1}{4}S_{ABCD}=\frac{1}{4}\)
\(\Rightarrow S_{BQM}=\frac{1}{3}S_{OBC}=\frac{1}{12}\)
\(\Leftrightarrow S_{MQDC}=S_{BCD}-S_{BQM}=\frac{1}{2}-\frac{1}{12}=\frac{5}{12}\)
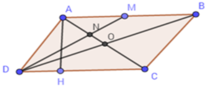
Cho hình bình hành ABCD có CD=4cm, đường cao vẽ từ AH đến cạnh CD bằng 3cm.
a, Tính diện tích nình bình hành ABCD.
b, Gọi M là trung điểm của AB. Tính diện tích △ADM.
c, DM cắt AC tại N. Chứng minh DN=2NM.
d, Tính diện tích △AMN.