tìm x thuộc z
1<|x-2|<4
nhanh hộ mình trong tối nay nha mình k cho
Cho đường thẳng d : x - 1 2 = y + 1 - 1 = z 1 và các điểm A(1;-1;2), B(2;-1;0). Tìm tọa độ điểm M thuộc đường thẳng d sao cho tam giác AMB vuông tại M
![]()
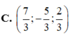
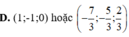
z, z1, z2 thuộc C
|z-z1|+|z-z2|=2a
Gọi 2c=|z1-z2| (0 <c <a)
Chứng minh rằng:
|w+2c^2|+|w-2c^2|=4ac
với z= w/(z2-z1) + (z1+z2)/2
Cho hai số phức z 1 , z 2 , thỏa mãn z 1 − i = z 2 − i = 13 v à z 1 − z 2 = 10 . Biết tập hợp các điểm biểu diễn số phức w = z 1 + z 2 trong mặt phẳng tọa độ Oxy thuộc một đường tròn (T) cố định. Tính chu vi của (T).
A. 12 π
B. 24 π
C. 48 π
D. 36 π
Tìm số thực x,y để hai số phức z1 = 9y2 - 4 - 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau? z 1 = 9 y 2 - 4 - 10 x i 5 v à z 2 = 8 y 2 + 20 i 11 l à
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Cho 2 số phức z 1 , z 2 có điểm biểu diễn lần lượt là M1, M2, cùng thuộc đường tròn có phương trình x 2 + y 2 = 1 và z 1 - z 2 = 1 . Tính giá trị biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
Cho hai số phức z 1 , z 2 có điểm biểu diễn lần lượt là M 1 , M 2 cùng thuộc đường tròn có phương trình x 2 + y 2 = 1 và z 1 - z 2 = 1 . Tính giá trị biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
Cho hai số phức z 1 , z 2 có điểm biểu diễn lần lượt là M 1 , M 2 cùng thuộc đường tròn có phương trình x 2 + y 2 = 1 và z 1 - z 2 = 1 . Tính giá trị biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
Cho phương trình a.z² +b.z+c=0 với a khác 0; a,b,c thuộc R không có nghiệm thực. Gọi z1, z2 là các nghiệm phức của phương trình và |(z1)²|+|(z2)²|=10. Tính z1.z2
Đặt \(z_1=x+yi\Rightarrow z_2=x-yi\)
\(\Rightarrow z_1z_2=x^2+y^2\)
\(\left|z_1^2\right|+\left|z_2^2\right|=10\Leftrightarrow\left|\left(x+yi\right)^2\right|+\left|\left(x-yi\right)^2\right|=10\)
\(\Leftrightarrow\left|x^2-y^2+2xyi\right|+\left|x^2-y^2-2xyi\right|=10\)
\(\Leftrightarrow\sqrt{\left(x^2-y^2\right)^2+4x^2y^2}+\sqrt{\left(x^2-y^2\right)^2+4x^2y^2}=10\)
\(\Leftrightarrow\left(x^2-y^2\right)^2+4x^2y^2=25\)
\(\Leftrightarrow\left(x^2+y^2\right)^2=25\)
\(\Leftrightarrow x^2+y^2=5\)
z, z1, z2, z3 thuộc C thỏa |z|=|z1|=|z2|=|z3|=10 (z1#z2#z3)
(z-3+4i)(thanh ngang của (z1-z2)); (z-3+4i)(thanh ngang của (z2-z3)); (z-3+4i)(thanh ngang của (z3-z1)) là thuần ảo
Tìm max P= |z-z1|^2+|z-z2|^2+|z-z3|^2
Ai cứu mình với!
Cho hai số phức z 1 , z 2 có điểm biểu diễn lần lượt là M 1 , M 2 cùng thuộc đường tròn có phương trình x 2 + y 2 = 1 và z 1 − z 2 = 1. Tính giá trị của biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
Đáp án D
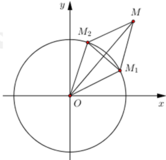
Tập hợp điểm biểu diễn số phức z 1 , z 2 là đường tròn tâm O, R = 1
Gọi M 1 z 1 , M 2 z 2 ⇒ O M 1 = O M 2 = 1
Ta có z 1 − z 2 = O M 1 → − O M 2 → = M 1 M 2 → = 1 ⇒ Δ O M 1 M 2 đều
Mà z 1 + z 2 = O M 1 → + O M 2 → = O M → = O M với M là điểm thỏa mãn O M 1 M M 2 là hình thoi cạnh 1 ⇒ O N = 3 ⇒ P = 3