Cho đường tròn (O, Đ) điểm A nằm ngoài đường tròn OA = 2R vẽ tiếp tuyến AB; AC (B, C là tiếp điểm)
a) Chứng minh AB ACb) Chứng minh tâm giâc ABC đềuc) Đường thẳng OA cắt đường tròn (O) tại M, N. Chứng minh ABNC là hình thoi
Những câu hỏi liên quan
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BCa) Chứng minh OA vuông góc với BC tại Hb) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.ADAH.AOc) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm...
Đọc tiếp
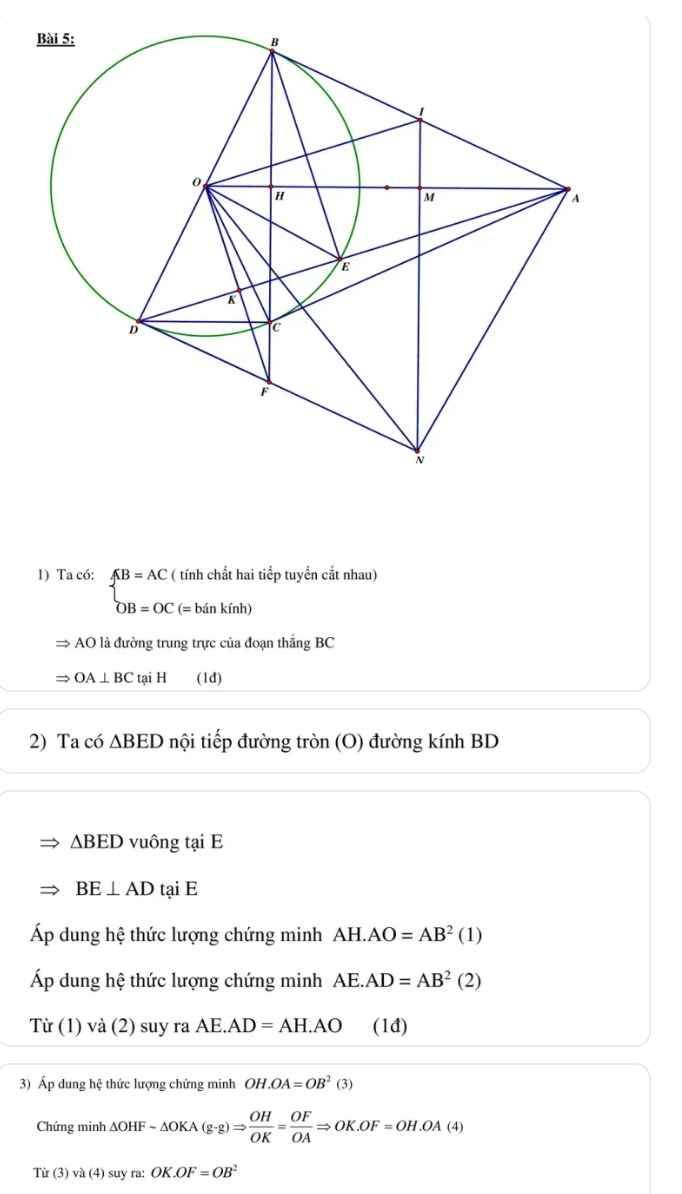
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC
a) Chứng minh OA vuông góc với BC tại H
b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.AD=AH.AO
c) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm (O)
d) Gọi I là trung điểm cạnh AB, qua I vẽ đừng thẳng vuông góc với cạnh AO tại M và đường thẳng này cắt đường thẳng DF tại N. Chứng minh: ND=NA
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O) .Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H giao điểm của OA và BC.a, Chứng minh OA vuông góc với BC tại Hb. Từ B vẽ đường kính BD của (O). đường thẳng AD cắt (O) tại E ( khác D).Chứng minh AE.AD AH. AOc.Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của (O).
Đọc tiếp
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O) .Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H giao điểm của OA và BC.
a, Chứng minh OA vuông góc với BC tại H
b. Từ B vẽ đường kính BD của (O). đường thẳng AD cắt (O) tại E ( khác D).Chứng minh AE.AD = AH. AO
c.Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của (O).
a) Do AB và AC là các tiếp tuyến cắt nhau tại A nên áp dụng tính chất hai tiếp tuyến cắt nhau ta có: AB = AC và AH là phân giác góc BAC.
Xét tam giác cân ABC có AH là phân giác nên AH đồng thời là đường cao. Vậy thì AO vuông góc với BC tại H.
b) Xét tam giác AEC và ACD có :
\(\widehat{A}\) chung
\(\widehat{ACE}=\widehat{ACD}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
\(\Rightarrow\Delta AEC\sim\Delta ACD\left(g-g\right)\)
\(\Rightarrow\frac{AE}{AC}=\frac{AC}{AD}\Rightarrow AE.AD=AC^2\)
Xét tam giác vuông ACD, đường cao CH, ta có :
\(AH.AO=AC^2\) (Hệ thức lượng)
Vậy nên ta có : AE.AD = AH.AO
c) Xét tam giác vuông ABO, đường cao BH, ta có: AH.AO = BO2
Do BO = DO nên AH.AO = OD2
Lại có \(\Delta AKO\sim\Delta FHO\left(g-g\right)\Rightarrow\frac{AO}{FO}=\frac{OK}{OH}\Rightarrow OK.OF=AO.OH\)
Vậy nên OK.OF = OD2 hay \(\frac{OK}{OD}=\frac{OD}{OF}\)
Vậy nên \(\Delta OKD\sim\Delta ODF\left(c-g-c\right)\Rightarrow\widehat{FDO}=\widehat{DKO}=90^o\)
Vậy nên FD là tiếp tuyến của đường tròn (O).
Đúng 1
Bình luận (0)
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.a, cho biết R5cm, OM3cm. Tính độ dài dây EH.b, Chứng minh AH là tiếp tuyến đường tròn(O)c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tu...
Đọc tiếp
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.
a, cho biết R=5cm, OM=3cm. Tính độ dài dây EH.
b, Chứng minh AH là tiếp tuyến đường tròn(O)
c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.
d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tuyến thứ 2 với đường tròn(O), cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q. Chứng minh AE=DQ
cho đường tròn 0 . từ điểm A nằm ngoài 0 vẽ tiếp tuyến AB , AC với O . vẽ đường kính BD. Tiếp tuyến tại D của O cắt BC tại E. Chứng minh ABOC nội tiếp
Cho đường tròn tâm (O) điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp diểm)
a) Chứng minh rắng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh BD song song với OA.
c) Tính đội dài các cạnh cùa tam giác ABC; biết OB= 2cm; OA=4cm.
Cho A là một điểm nằm ngoài đường tròn left(O;Rright). Qua A vẽ hai tiếp tuyến AB, AC (B, C là tiếp điểm). H là giao điểm của AO và BC. Kẻ đường kính BD; AD cắt left(Oright) tại E.a. Chứng minh: OA perp BC và CD // OA.b. Chứng minh: AH.AO AE.AD và ∠AHE ∠ADO.c. Cho OB 2cm, OA 4 cm. Chứng minh: △ABC là tam giác đều và tính diện tích △ABC
Đọc tiếp
Cho A là một điểm nằm ngoài đường tròn \(\left(O;R\right)\). Qua A vẽ hai tiếp tuyến AB, AC \((\)B, C là tiếp điểm\()\). H là giao điểm của AO và BC. Kẻ đường kính BD; AD cắt \(\left(O\right)\) tại E.
a. Chứng minh: OA \(\perp\) BC và CD // OA.
b. Chứng minh: AH.AO \(=\) AE.AD và ∠AHE \(=\) ∠ADO.
c. Cho OB = 2cm, OA = 4 cm. Chứng minh: △ABC là tam giác đều và tính diện tích △ABC
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD tại C
Ta có: BC\(\perp\)CD
OA\(\perp\)BC
Do đó: OA//CD
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(3\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{EAH}\) chung
Do đó: ΔAEH đồng dạng với ΔAOD
=>\(\widehat{AHE}=\widehat{ADO}\)
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Xét ΔOBA vuông tại B có \(BO^2+BA^2=OA^2\)
=>\(BA^2+2^2=4^2\)
=>\(BA^2=12\)
=>\(BA=2\sqrt{3}\left(cm\right)\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{ABC}=\left(2\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=12\cdot\dfrac{\sqrt{3}}{4}=3\sqrt{3}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho 2 đường tròn đồng tâm, tâm O bán kính R và tâm O bán kính R' (R>R'). Điểm M nằm ngoài 2 đường tròn. Vẽ MA là tiếp tuyến của đường tròn tâm O bán kính R. MB là tiếp tuyến của đường tròn tâm O bán kính R'. Chứng minh rằng đường trung trực của đoạn thẳng AB đi qua trung điểm của OM
cho điểm M nằm ngoài (O;R), vẽ các tiếp tuyến MA,MB với (O;R).Vẽ đường kính AC, tiếp tuyến tại C của đường tròn (O;R) cắt AB ở D.Chứng minh rằng: a)Tứ giác MAOB nội tiếp b)AB.AD=4R^2
a) Xét tứ giác MAOB có:
\(\widehat{MAO}+\widehat{MBO}=90^o+90^o=180^o\) (MA,MB là tiếp tuyến)
=> Tứ giác MAOB nội tiếp (dhnb)
b) Tam giác CAD vuông tại C (tiếp tuyến tại C) và có BC là đường cao (góc ABC nội tiếp chắn nửa đường tròn)
\(\Rightarrow AC^2=AB.AD\) (hệ thức lượng) (1)
Có: \(AC^2=\left(2R\right)^2=4R^2\) (2)
Từ (1) và (2) suy ra \(AB.AD=4R^2\)
Đúng 1
Bình luận (0)
a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
ΔABC nội tiếp đường tròn(A,C,B∈(O))
AC là đường kính(gt)
Do đó: ΔABC vuông tại B(Định lí)
⇔CB⊥AB tại B
⇔CB⊥AD tại B
Áp dụng hệ thức lượng trong tam giác vuông vào ΔADC vuông tại C có CB là đường cao ứng với cạnh huyền AD, ta được:
\(AB\cdot AD=AC^2\)
\(\Leftrightarrow AB\cdot AC=\left(2\cdot R\right)^2=4R^2\)(đpcm)
Đúng 1
Bình luận (0)
Từ một điểm A nằm ngoài đường tròn [O,R] ta vẽ hai tiếp tuyến AB,AC với đường tròn [ B,C là hai tiếp điểm ] . trên cung nhỏ BC lấy một điểm M, vẽ MI vuông góc với AB, MK vuông góc với AC [ I thuộc AB ,K thuộc AC ]