Trên mặt phẳng tọa độ Oxy, cho parabol (P): y = -3x23x2 và hai điểm A(-1;-3), B(2;3)
a) Chứng tỏ rằng điểm A thuộc parabol (P).
b) Tìm tọa độ điểm C (C khác A) thuộc parabol (P) sao cho ba điểm A, B, C thẳng hàng.
Trong mặt phẳng tọa độ Oxy, cho parabol (P):y=x2 . Gọi A, B là hai điểm trên parabol có
hoành độ tương ứng là 1 và 2. Tìm tọa độ hình chiếu vuông góc của gốc tọa độ O lên đường
thẳng AB.
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
vậy: A(1;1); B(2;4)
Gọi H là tọa độ của hình chiếu vuông góc kẻ từ O xuống AB
O(0;0); H(x;y); A(1;1); B(2;4)
\(\overrightarrow{OH}=\left(x;y\right);\overrightarrow{AB}=\left(1;3\right)\)
Vì OH vuông góc với AB nên \(x\cdot1+y\cdot3=0\)
=>x+3y=0
Ta có: \(\overrightarrow{AH}=\left(x-1;y-1\right);\overrightarrow{AB}=\left(1;3\right)\)
mà A,H,B thẳng hàng
nên \(\dfrac{x-1}{1}=\dfrac{y-1}{3}\)
=>3x-3=y-1
=>3x-y=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-y=2\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y=6\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}10x=6\\x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\3y=-x=-\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(H\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = - x2
a) Vẽ parabol (P)
b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y = - x – 2 và (P).
c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại M
Bài 2 Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
CMR: (d) luôn cắt (P) tại 2 điểm phân biệt
a) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P = ![]() khi m thay đổi
khi m thay đổi
Bài 3. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt nằm bên phải trục tung
Bài 4. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Bài 5. Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1
Tìm m sao cho (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 sao cho ![]()
Bài 6. Cho parabol (P) : y = ![]() x2 và đường thẳng (d) : y = mx -
x2 và đường thẳng (d) : y = mx - ![]() m2 + m +1.
m2 + m +1.
a) Với m = 1, xác định tọa độ các giao điểm A, B của (d) và (P).
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao cho ![]() .
.
Trên mặt phẳng tọa độ Oxy , hai điểm A và B chạy tên parabol (P): y=x2 sao cho A,B không trùng với tọa độ O và OA vuông góc với OB. Đường thẳng AB luôn đi qua điểm cố định có tọa độ là .........
Trong mặt tọa độ Oxy, cho đường thẳng (d): y = 2x + m2 – m + 5 và parabol (P): y = x2 . a. Với m = 1, vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ Oxy. b. Chứng minh đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi m. c. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn (x1 + 1)(x2 + 1) = –2. d*. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn |2x1| – |x2| = 1.
trên mặt phẳng tọa độ Oxy cho điểm M nằm trên parabol(P):y=\(x^2\)và điểm A(0;3). Xác định tọa độ điểm M sao cho độ dài AM ngắn nhất
Trong mặt phẳng Oxy cho parabol ( P ) : y = 1 4 x 2 và đường thẳng d : y = x + 3.
1) Vẽ (P) và d trên cùng một hệ trục tọa độ.
2) Tìm tọa độ giao điểm của (P) và d.
1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
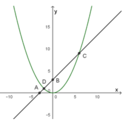
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .
Trong mặt phẳng tọa độ oxy cho parabol p y = x bình và đường thẳng d có dạng y = mx + m+1 a) với m =1 Tìm tọa độ giao điểm của đường thẳng d với hai trục tọa độ b) tính giá trị của m để đường thẳng d cắt parabol p tại 2 điểm phân biệt nằm về bên trái của đường thẳng x = 2
Trong mặt phẳng tọa độ Oxy, cho parabol (p) : y=\(-\dfrac{x^2}{2}\)và đường thẳng (d): y=x+m
a) Tìm tọa độ điểm M thuộc parabol (P) biết điểm M có tung độ bằng -2
b,Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm A\(\left(x_1,M_1\right)\),B\(\left(x_2,y_2\right)\)
phân biệt thỏa mãn \(x_1x_2+x_1+x_2=10\)
giúp mk câu này với ạ
1. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(0;2), B(4;2). Tìm điểm M trên đoạn thẳng AB để parabol (P) đỉnh O và đi qua điểm M chia tam giác vuông OAB thành hai phần có diện tích bằng nhau.
2. Cho hình phẳng (H ) giới hạn bởi các đường \(y=x^2,y=2x\) . Gọi S là tập hợp các giá trị của tham số thực k để đường thẳng x = k2 chia hình phẳng (H) thành hai phần có diện tích bằng nhau. Hỏi tập hợp S có bao nhiêu phần tử?