Cho tam giác ABC có \(\widehat{B}-\widehat{C}=a.\)Tia phân giác của \(\widehat{BAC}\)cắt BC ở D.
a) Tính \(\widehat{ADC}\)và \(\widehat{ADB}\)
b) Vẽ \(AH\perp BC\)( \(H\in BC\)). Tính \(\widehat{HAD}\)
Những câu hỏi liên quan
cho tam giác ABC có\(\widehat{B}-\widehat{C}=\alpha\). Tia phân giác của góc a cắt BC ở D.
a)Tính \(\widehat{ADC},\widehat{ADB}\)
b)Vẽ AH vuông góc với BC , tính \(\widehat{HAD}\)
Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\).
b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\).
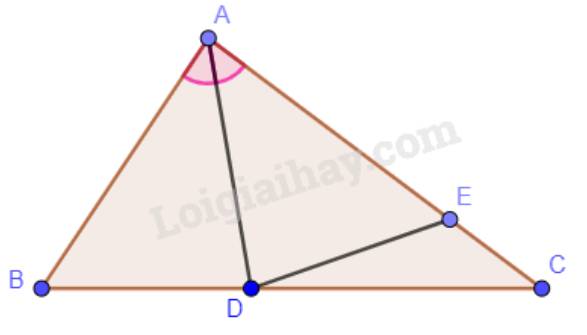
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).
Đúng 0
Bình luận (0)
1.Cho hai đoạn thẳng AB và CD cắt nhau tại E. Các tia phân giác của widehat{ACE} và widehat{DBE} cắt nhau tại K. CMR: 2.widehat{BKC}widehat{BAC}+widehat{BDC}2. Cho tam giác ABC có widehat{ABC}-widehat{ACB}60^o . Tia phân giác của widehat{A} cắt BC tại D.a) Tính số đo của widehat{ADC} và widehat{ADB}b) Vẽ AHperp BC tại H. Tính số đo của widehat{HAD}
Đọc tiếp
1.Cho hai đoạn thẳng AB và CD cắt nhau tại E. Các tia phân giác của \(\widehat{ACE}\) và \(\widehat{DBE}\) cắt nhau tại K. CMR: \(2.\widehat{BKC}=\widehat{BAC}+\widehat{BDC}\)
2. Cho tam giác \(ABC\) có \(\widehat{ABC}-\widehat{ACB}=60^o\) . Tia phân giác của \(\widehat{A}\) cắt BC tại D.
a) Tính số đo của \(\widehat{ADC}\) và \(\widehat{ADB}\)
b) Vẽ \(AH\perp BC\) tại H. Tính số đo của \(\widehat{HAD}\)
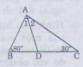
Cho tam giác ABC có \(\widehat{B}=80^0,\widehat{C}=30^0\). Tia phân giác của góc A cắt BC ở D. Tính \(\widehat{ADC},\widehat{ADB}\) ?
\(\widehat{BAC}\)= 1800 - (\(\widehat{B}+\widehat{C}\)) = 1800 - ( 800 + 300)= 700
\(\widehat{A}_1\)=\(\widehat{A}_2\)=\(\dfrac{\widehat{A}}{2}\)=\(\dfrac{70^0}{2}\)= 350
\(\widehat{ADC}=\widehat{B}+\widehat{A}_1\)(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó \(\widehat{ADB}\)= 1800 - \(\widehat{ADC}\)= 1800 + 1150=650
Đúng 0
Bình luận (0)
Hình vẽ: 
Gọi A1, A2 là 2 góc được tạo ra bởi tia phân giác góc A.
Ta có:
Góc ∠BAC = 1800 – ( ∠B + ∠C)
= 1800 – ( 800 + 300) = 700
Hay ta có thể gọi ∠A = 700
Góc ∠A1 = ∠A2
= ∠A/2 = 700 /2 = 350
Xét tam giác ADC ta có: Góc ∠ADC = 1800 – (∠C + ∠A2)= 1800 – (350 + 300)= 1150
Do đó góc ∠ADB = 1800 – ∠ADC= 1800 – 1150
= 650
Đúng 0
Bình luận (0)
Giải:
ˆBACBAC^= 1800 - (ˆBB^+ˆCC^) = 1800 - ( 800 + 300)= 700
ˆA1A1^=ˆA2A2^=ˆA2A^2=70027002= 350
ˆADCADC^=ˆBB^+ˆA1A1^(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó ˆADBADB^= 1800 - ˆADCADC^= 1800 + 1150=650
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có \(\widehat{ABC}-\widehat{ACB}=60^o\). Tia phân giác của góc A cắt BC tại D
a) Tính số đo của các góc ADC và ADB
b) Vẽ AH vuoong góc với BC tại H. Tính sô đo của góc HAD
Help me !!!1
Cho tam giác ABC có \(\widehat{B}=70^o,\widehat{C}=30^o\).Tia phân giác của\(\widehat{A}\)cắt BC tại D.Kẻ AH vuông góc với BC\(\left(H\in BC\right)\).
a,tính\(\widehat{BAC}\)
b,tính\(\widehat{ADH}\)
c,tính\(\widehat{HAD}\)
Cho tam giác ABC có \(\widehat{B}-\widehat{C}=20^0\). Tia phân giác của góc A cắt BC ở D.
Tính số đo các góc \(\widehat{ADC},\widehat{ADB}\) ?
Ta có :
A+B+C=180(tính chất của một tam giác)
⇒A=180-B-C
⇒A=180-20
⇒A=160
vì tia phân giác của góc A cắt BC tại D nên A1=A2=\(\dfrac{160}{2}\)=80
\(\Leftrightarrow\)D1=80
Vì góc D1 và góc D2 là 2 góc kề bù nên D1+D2=180
mà góc D1=80
\(\Rightarrow\)D2=180-80
\(\Rightarrow\)D2=100
Vay : D1=80, D2=100
mk ko viết đc kí hiệu góc và độ mong mọi người thông cảm
Đúng 0
Bình luận (1)
Cho tam giác ABC có \(\widehat{B}=70^0,\widehat{C}=30^0\). Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (\(H\in BC\))
a) Tính \(\widehat{BAC}\) ?
b) Tính \(\widehat{ADH}\) ?
c) Tính \(\widehat{HAD}\) ?
cho tam giác ABC, widehat{B} widehat{C}, AD là tia phân giác trong, AE là tia phân giác ngoài đỉnh Aa) chứng minh widehat{ADC}-widehat{ADB}widehat{B}-widehat{C}b) kẻ AH vuông góc với BC, H nằm trên đoạn thẳng BC. Chứng minh widehat{AEB}widehat{HAD}frac{widehat{B}-widehat{C}}{2}c) cho widehat{B}-widehat{C}40 độ. Tính widehat{ADB}widehat{ADC}widehat{HAD}
Đọc tiếp
cho tam giác ABC, \(\widehat{B}\) >\(\widehat{C}\), AD là tia phân giác trong, AE là tia phân giác ngoài đỉnh A
a) chứng minh \(\widehat{ADC}\)-\(\widehat{ADB}\)=\(\widehat{B}\)-\(\widehat{C}\)
b) kẻ AH vuông góc với BC, H nằm trên đoạn thẳng BC. Chứng minh \(\widehat{AEB}\)=\(\widehat{HAD}\)=\(\frac{\widehat{B}-\widehat{C}}{2}\)
c) cho \(\widehat{B}\)-\(\widehat{C}\)=40 độ. Tính \(\widehat{ADB}\)\(\widehat{ADC}\)\(\widehat{HAD}\)