\(\widehat{xAB}+\widehat{yBA}=180^o\) (trong cùng phía)

\(\Rightarrow\widehat{yAB}=180^o-60^o=120^o\)

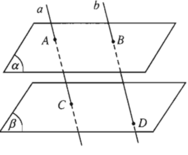
Sai vì

Ta có định lí 3 trang 67: cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song

Theo đề bài ta có: (α) // (β)

a//b nên A,B,C,D thuộc mặt phẳng

AB là giao tuyến của (α) và (ABDC)

CD là giao tuyến của (β) và (ABDC)

⇒ AB // CD (theo định lí)

Hình 2.72 không biểu diễn được AB // CD

Ta có (P) // (Q)

Suy ra AA’ // BB’ (1)

Ta có a // b

Suy ra AB // A’B’ (2)

Từ (1) và (2) suy ra AA’B’B là hình bình hành

Do đó AB = A’B’

a, Nếu tia At không cắt yy'

=> At // yy'

=> At trung với Ax (vì xx' // yy')

Mà At là phân giác góc xAb

=> At nằm giữa Ax và AB

=> At không trùng Ax

=> At cắt yy'

b, 

Bạn xem lại đề. C ở đâu vậy?

Ta có :\(M2+M\widehat{1}=180^0\)

\(55^0+\widehat{M1}=180^0\)

\(M\widehat{1}=180^0-55^0\)

\(\widehat{M1}=125^0\)

TA CÓ :\(\widehat{M3}=\widehat{M1}=125^0\)(hai góc đối đỉnh)

         \(\widehat{M4}=\widehat{M2}=55^0\)(hai góc đối đỉnh)

          \(\widehat{N3}=\widehat{M3}=125^0\)(hai góc so le trong)(yy'//zz')

           \(\widehat{N1}=\widehat{M4}=55^0\)(hai góc so le trong)(yy'//zz')

          \(\widehat{N2}=\widehat{N3}=125^0\)(hai góc đối đỉnh)

           \(\widehat{N4}=\widehat{N1}=55^0\)(hai góc đối đỉnh)

HỌC TỐT <3

thank nha

hông có j ^^

+ Xét \(\Delta ABC\)có :

\(DE//BC\left(gt\right)\)

\(\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)( định lí Ta - lét ) (1)

+ Xét \(\Delta DBC\)có :

\(AK//BC\left(gt\right)\)

\(\Rightarrow\frac{AK}{BC}=\frac{AD}{DB}\)( định lí Ta - lét ) (2)

+ Xét \(\Delta BEC\)có:

\(AG//BC\left(gt\right)\)

\(\Rightarrow\frac{AG}{BC}=\frac{AE}{EC}\)( định lí Ta - lét ) (3)

Từ (1) , (2) và (3) \(\Rightarrow\frac{AK}{BC}=\frac{AG}{BC}\)

\(\Rightarrow AK=AG\)

\(\Rightarrow A\)là trung điểm của KG (đpcm)

Chúc bạn học tốt !!!