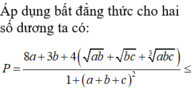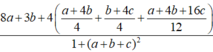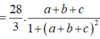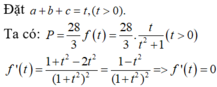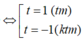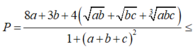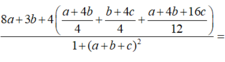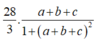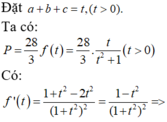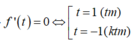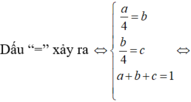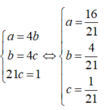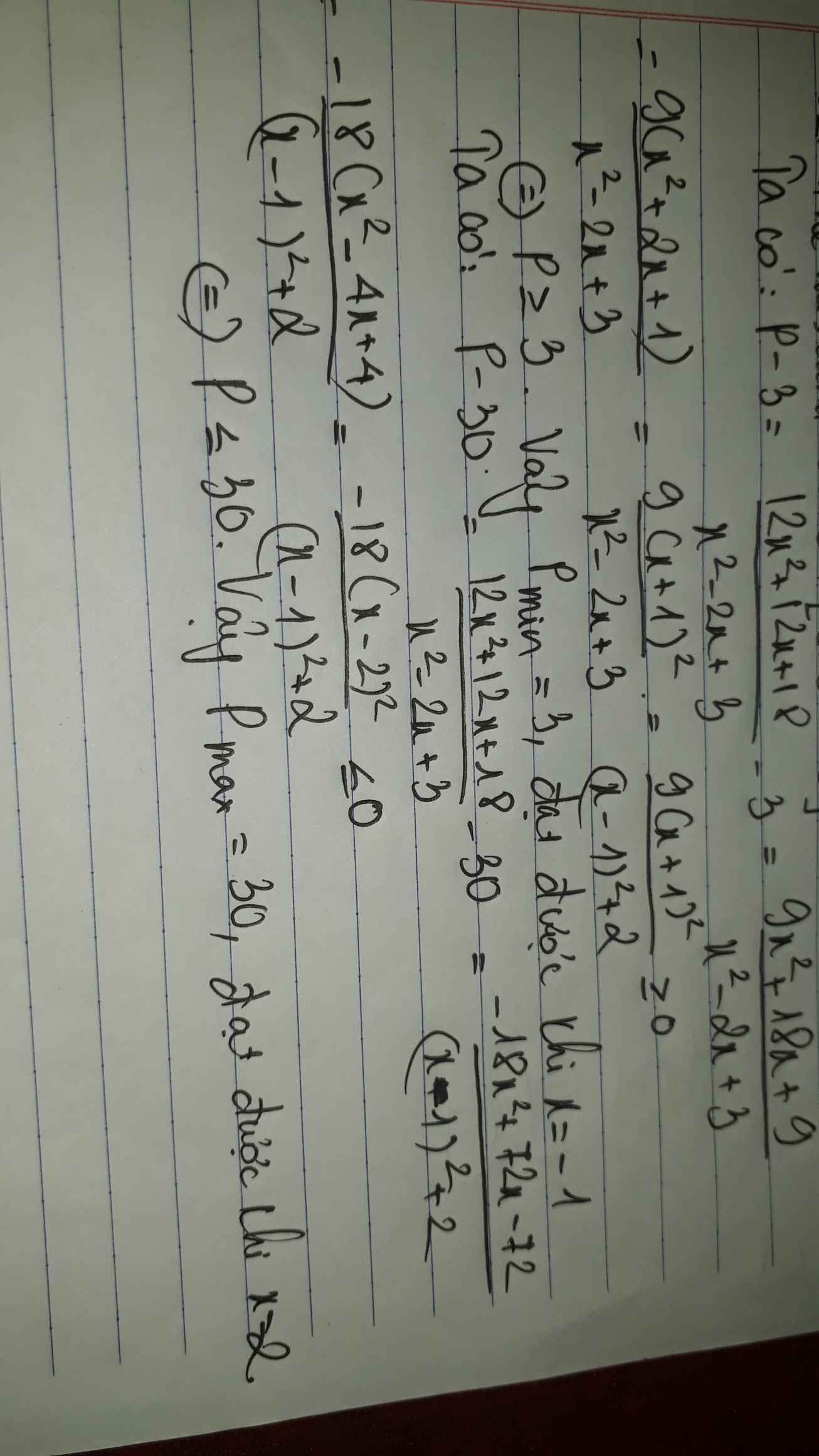Tìm giá trị lớn nhất của biểu thức P=18−|x+3|
Đáp án: max P=

Những câu hỏi liên quan
Tìm giá trị lớn nhất của biểu thức
\(-\left(\frac{4}{9}x-\frac{2}{15}\right)^6+3\)
(đáp án và cách giải)
\(-\left(\frac{4}{9}x-\frac{2}{15}\right)^6+3\)
\(=3-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\le3\)
Max \(=3\)
Đúng 0
Bình luận (0)
giá trị lớn nhất của biểu thức B=\(\frac{3,3}{1,5+x^2}\)
mk chỉ cần đáp án
tìm giá trị lớn nhất của biểu thức A=18-3/x/
Ta có :
\(\left|x\right|\ge0\)
\(\Rightarrow3\left|x\right|\ge0\)
\(\Rightarrow A=18-3\left|x\right|\le18-0=18\)
Do đó GTLN của A là 18
Dấu bằng xảy ra khi \(\left|x\right|=0\Rightarrow x=0\)
Vậy ...
Đúng 0
Bình luận (0)
|x| luôn luôn lớn hơn hoặc bằng 0 vs mọi x
Nên 3|x| có giá trị nhỏ nhất là 0
Vậy A có giá trị lớn nhất là : A = 18 - 0 = 18
Đúng 1
Bình luận (0)
câu 1 :tìm giá trị nguyên dương thỏa mãn I x - 1 I = - ( x - 1 ) Đáp số :............
câu 2 : tìm giá trị lớn nhất của biểu thức 15 - ( x - 2 )2 Đáp số :.............
câu 3 : tìm giá trị x thỏa mãn x - 5 < 0 và 3 - x < 0
câu 1 dễ bn tự làm nhé
câu 2 nhận xét (x-2)^2 >=0
=> 15-(x2)^2 >= 15
dấu = xảy ra khi và chỉ khi
x-2 = 0
=> x= 2
câu 3 x-5 <0
=> x < 5 (1)
3-x <0
=> x>3 (2)
từ (1) và (2) => 3< x< 5
=> x= 4
Đúng 0
Bình luận (0)
câu 1: x=1
câu 2: vì \(^{\left(x-2\right)^2}\)\(\ge\)0
=> 15-\(\left(x-2\right)^2\)\(\le\)0
Dấu "=" xảy ra <=> x-2=0
<=> x=2
Câu 3: x-5 < 0 => x<5
và 3-x >0 =>x>3
=> 3<x<5
Đúng 0
Bình luận (0)
câu 1 x = 1 bạn thay thử bít
câu 2 x = 2 => đáp số = 15 là lớn nhất
câu 3 x thoả mãn là số 4
thấy hay cho mk điểm nhé ! chúc hc tốt
Đúng 0
Bình luận (0)
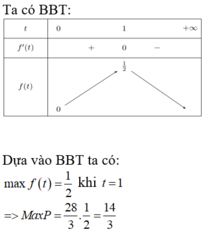
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức gần với giá trị nào nhất trong các đáp án sau: A. 4,65 B. 4,66 C. 4,67 D. 4,64
Đọc tiếp
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức 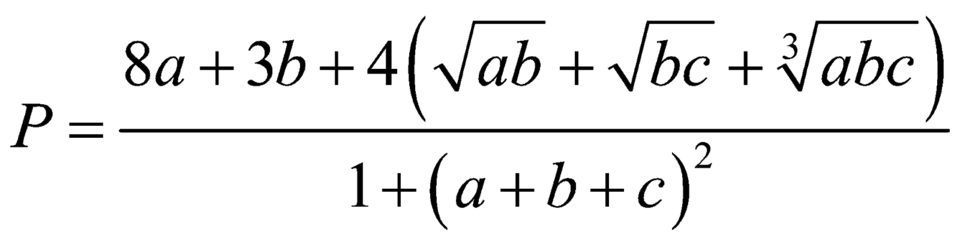 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
A. 4,65
B. 4,66
C. 4,67
D. 4,64
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức 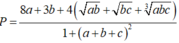 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
A. 4,65
B. 4,66
C. 4,67
D. 4,64
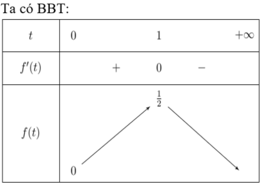
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
\(P=\dfrac{12x^2+12x+18}{x^2-2x+3}\)
tìm số tự nhiên y để biểu thức A = 218 - ( 2 x Y -18) có giá trị lớn nhất và tìm giá trị lớn nhất của A
1) tìm giá trị nhỏ nhất của biểu thức:
A=/x-3/+8.
2) tìm giá trị nhỏ nhất của biểu thức:
B= 11- / 4+x /
3) tìm giá trị nhỏ nhất của biểu thức:
a) M=/x-3/+18-x/
b) M= /x-4/+/x-10/
2:
|x+4|>=0
=>-|x+4|<=0
=>B<=11
Dấu = xảy ra khi x=-4
Đúng 0
Bình luận (0)