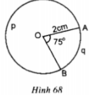
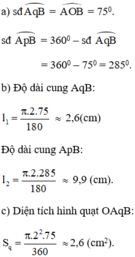Tính diện tích hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o.

Những câu hỏi liên quan
Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:
Hình tròn bán kính R (ứng với cung 360o) có diện tích là … .
Vậy hình quạt tròn bán kính R, cung 1o có diện tích là … .
Hình quạt tròn bán kính R, cung no có diện tích S = … .
Hình tròn bán kính R (ứng với cung 360o) có diện tích là πR2
Vậy hình quạt tròn bán kính R, cung 1o có diện tích là (πR2)/360
Hình quạt tròn bán kính R, cung no có diện tích S = (πR2n)/360
Đúng 0
Bình luận (0)
Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:Hình tròn bán kính R (ứng với cung
360
°
) có diện tích là … .Vậy hình quạt tròn bán kính R, cung
1
°
có diện tích là … .Hình quạt tròn bán kính R, cung
n
°
có diện tích S … .
Đọc tiếp
Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:
Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là … .
Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là … .
Hình quạt tròn bán kính R, cung n ° có diện tích S = … .
Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là π R 2
Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là π R 2 / 360
Hình quạt tròn bán kính R, cung n ° có diện tích S = π R 2 n / 360
Đúng 0
Bình luận (0)
cho tam gíc ABC nội tiếp đường tròn (O) bán kính R có góc C = 45 độ
a. tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b. tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
Một hình quạt tròn bán kính R=4/√π, cung 90°. Tính diện tích hình quạt đó
S quạt = \(\dfrac{\pi.R^{2^{ }}.n^o}{360}\)=\(\dfrac{\pi.\left(\dfrac{4}{\sqrt{\pi}}\right)^2.90}{360}\)=4(đ/v diện tích)
Đúng 1
Bình luận (0)
Nêu cách tính diện tích hình quạt tròn bán kính R, cung no.
Diện tích S của hình quạt tròn bán kính R, cung no được tính theo công thức:
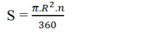
Đúng 0
Bình luận (0)
Nêu cách tính diện tích hình quạt tròn bán kính R, cung no.
Diện tích S của hình quạt tròn bán kính R, cung no được tính theo công thức:
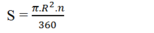
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R=3 cm và hai điểm A,B nằm trên đường tròn (O) sao cho số đo cung lớn bằng 240°. Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB vsf cung nhỏ AB.
Tính diện tích một hình quạt tròn có bán kính 6 cm, số đo cung là 36o.
Theo công thức S = ta có S=
≈ 3,6π (cm2)
Đúng 0
Bình luận (0)
Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là 36o Đáp án và hướng dẫn giải bài 79: Diện tích hình quạt ∠OAB có OA = 6cm, cung AOB =36o Theo công thức S = ΠR2no/360o Ta có S= Π62.36/360 ≈ 3,6π = 11,30(cm2)
Đúng 0
Bình luận (0)
Theo công thức S = ta có S=
≈ 3,6π (cm2)
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM 2cm và CD
4
3
cm. Tính:a, Độ dài đường tròn (O) và diện tích đường tròn (O)b, Độ dài cung
C
A
D
⏜
và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ
C...
Đọc tiếp
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM = 2cm và CD = 4 3 cm. Tính:
a, Độ dài đường tròn (O) và diện tích đường tròn (O)
b, Độ dài cung C A D ⏜ và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ C D ⏜
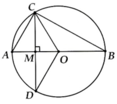
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2
Đúng 1
Bình luận (0)
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc A O B = 75 °
a) Tính sđ góc ApB
b) Tính độ dài hai cung AqB và ApB
c) Tính diện tích hình quạt tròn OAqB