Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.

Những câu hỏi liên quan
Cho đường tròn tâm O và dây BC không đi qua O. Điểm A chuyển động rên cung lớn . Vẽ đường tròn tâm I đi qua điểm B và tiếp xúc với AC tại A. Vẽ đường tròn tâm K đi qua điểm C và tiếp xúc với AB tại A.CMR:
a) 4 điểm B,D,O,C cùng thuộc 1 đường tròn.
b) Đường thẳng AD luôn đi qua 1 điểm cố định.
a) Ta có đuờng tròn (I) tiếp xúc với AC tại A, theo tính chất góc tạo bởi tiếp tuyến và dây thì ^DAC = ^DBA
Tuơng tự ^DAB = ^DCA. Do đó ^BDC = ^DAB + ^DAC + ^DBA + ^DCA = 2(^DAB + ^DAC) = 2.^BAC = ^BOC
Suy ra 4 điểm B,D,O,C cùng thuộc một đuờng tròn theo quỹ tích cung chứa góc (đpcm).
b) Gọi đuờng thẳng AD cắt đường tròn đi qua 4 điểm B,O,D,C tại S khác D. Ta sẽ chỉ ra S cố định.
Thật vậy, gọi Dx là tia đối của tia DB. Ta có ^ODC = ^OBC = ^OCB = ^ODx => DO là phân giác ^CDx
Ta thấy hai đuờng tròn (O) và (I) cắt nhau tại A và B nên OI vuông góc AB
Mà AK vuông góc với AB (vì (K) tiếp xúc AB tại A) nên OI // AK. Tuơng tự OK // AI
Từ đây tứ giác AIOK là hình bình hành => IK chia đôi OA. Cũng dễ thấy IK là trung trực của AD
Theo đó IK chứa đuờng trung bình của \(\Delta\)AOD => IK // OD. Mà IK vuông góc AD nên OD vuông góc AD
Kết hợp với OD là phân giác của ^CDx => AD là phân giác của ^BDC (do ^CDx và ^BDC bù nhau)
Hay DS là phân giác của ^BDC. Lại có ^BDC là góc nội tiếp đuờng tròn đi qua B,D,O,C
=> S là điểm chính giữa (BC không chứa O của đuờng tròn (BOC)
Vì B,O,C cố định nên điểm chính giữa (BC không chứa O của (BOC) cố định => S cố định
Vậy AD luôn đi qua S cố định (đpcm).
Đúng 0
Bình luận (0)
cho tam giác ABCnội tiếp đường tròn tâm o,AB<ACgọi M là một điểm di động trên cạnh BC vẽ đường tròn tâm P đi qua B và M và tiếp xúc với AB vẽ đường tròn tâm Q đi qua C và M và tiếp xúc với AChai đường tròn P và Q cắt nhau tại điểm thứ 2 là N
a)điểm N thuộc đường tròn (Q)
b)BP và CQ cắt nhau tại điểm D cố định
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại Da, Nêu cách vẽ đường tròn (I) nói trênb, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàngc, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
Đọc tiếp
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại D
a, Nêu cách vẽ đường tròn (I) nói trên
b, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàng
c, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
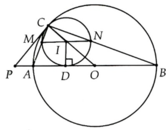
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm
Đúng 0
Bình luận (0)
Cho đường tròn ( O) và dây AB cố định, điểm M tuỳ ý thay đổi trên đoạn thẳng AB. Qua A, M dựng đường tròn tâm I tiếp xúc với đường tròn (O) tại A. Quan B, M dựng đường tròn tâm J tiếp xúc với (O) tại B. Hai đường tròn tâm I và tâm J cắt nhau tại điểm thứ hai là N. C/m
a)MN luôn đi qua một điểm cố định.
b)khi M chạy trên đoạn AB thì N chạy trên đoạn nào
a) Tiếp tuyến tại A và B của (O) cắt nhau tại C.CM cắt (I) tại N'
Xét \(\Delta CAM\) và \(\Delta CN'A:\) Ta có: \(\left\{{}\begin{matrix}\angle ACN'chung\\\angle CAM=\angle CN'A\end{matrix}\right.\)
\(\Rightarrow\Delta CAM\sim\Delta CN'A\left(g-g\right)\Rightarrow\dfrac{CA}{CN'}=\dfrac{CM}{CA}\Rightarrow CA^2=CM.CN'\)
mà \(CA^2=CB^2\Rightarrow CB^2=CM.CN'\Rightarrow\dfrac{CB}{CM}=\dfrac{CN'}{CB}\)
Xét \(\Delta CBM\) và \(\Delta CN'B:\) Ta có: \(\left\{{}\begin{matrix}\angle BCN'chung\\\dfrac{CB}{CM}=\dfrac{CN'}{CB}\end{matrix}\right.\)
\(\Rightarrow\Delta CBM\sim\Delta CN'B\left(c-g-c\right)\Rightarrow\angle CBB=\angle CN'B\Rightarrow N'\in\left(J\right)\)
\(\Rightarrow N\equiv N'\Rightarrow MN\) luôn đi qua điểm C mà A,B cố định
\(\Rightarrow C\) cố định \(\Rightarrow\) đpcm
b) mình chỉ chứng minh được N thuộc 1 đường tròn cố định thôi,còn chạy trên đoạn thẳng hình như là ko được
Ta có: \(\angle ANB=\angle ANM+\angle BNM=\dfrac{1}{2}\angle AIM+\dfrac{1}{2}\angle BJM\)
Xét \(\Delta AIM\) và \(\Delta AOB:\) Ta có: \(\left\{{}\begin{matrix}\angle OABchung\\\dfrac{IA}{OA}=\dfrac{IM}{OB}\end{matrix}\right.\)
\(\Rightarrow\Delta AIM\sim\Delta AOB\left(c-g-c\right)\Rightarrow\angle AIM=\angle AOB\)
Tương tự \(\Rightarrow\angle BJM=\angle AOB\)
\(\Rightarrow\angle ANB=\dfrac{1}{2}\angle AOB+\dfrac{1}{2}\angle AOB=\angle AOB\)
\(\Rightarrow N\in\left(AOB\right)\) mà A,O,B cố định \(\Rightarrow N\in\left(AOB\right)\) cố định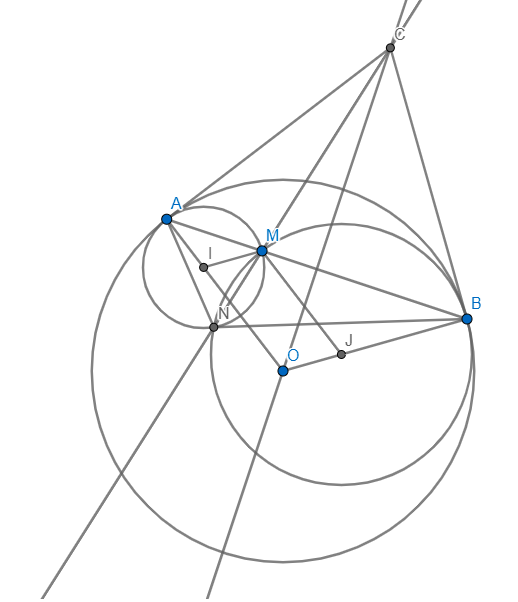
Đúng 1
Bình luận (1)
GIÚP EM VỚI Ạ,EM CẦN GẤP
Cho đường tròn tâm O,đường kính AB=2R.Lấy điểm M thuộc nửa đường tròn,vẽ (M) tiếp xúc AB tại H.Qua A và B vẽ hai tiếp tuyến AC,BD với (M) tại C,D.Chứng minh
a)3 điểm C,M,D thẳng hàng
b)CD là tiếp tuyến của(O) tại M.
c)Gọi giao điểm của CD,AB là K.chứng minh OK.OH=R^2
cho điểm a nằm ngoài đường tròn tâm o vẽ 2 tiếp tuyếnAM AN với đường tròn tâm (M N là các tiếp điểm) Vẽ các tuyến A C D không đi qua tâm o
chứng minh 5 điểm A M O N cùng thuộc 1 đường thẳng
Chứng minh FN.FA =FO.FH
Cho nửa đường tròn tâm O đường kính AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tiếp tuyến Ax, By. Lấy điểm M bất kì thuộc nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB tại H.a) Qua M kẻ tiếp tuyến với nửa đường tròn cắt Ax,By lần lượt tại C và D. Gọi I là giao điểm của AD và BC. Chứng minh M,I,H thẳng hàng.b) Vẽ đường tròn tâm (O) nội tiếp tam giác AMB tiếp xúc với AB ở K. Chứng minh SAMB AK.KB
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tiếp tuyến Ax, By. Lấy điểm M bất kì thuộc nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB tại H.
a) Qua M kẻ tiếp tuyến với nửa đường tròn cắt Ax,By lần lượt tại C và D. Gọi I là giao điểm của AD và BC. Chứng minh M,I,H thẳng hàng.
b) Vẽ đường tròn tâm (O') nội tiếp tam giác AMB tiếp xúc với AB ở K. Chứng minh SAMB= AK.KB
cho (O;R), đường kính AB cố định. Đường thẳng d tiếp xúc với đường tròn tâm O tại B. Đường kính MN thay đổi sao cho MN không vuông góc với AB và M ko trùng với A và B. Các đường thẳng AM và AN cắt đường thẳng d tại C và D. Gọi I là trung điểm của CD, H là giao điểm của AI và MN. Khi đường kính MN quay xung quanh O. Hãy chứng minh:a) AM.AC không đổib) bốn điểm C,M,N,D cùng nằm trên một đường tròn c) H thuộc một đường cố địnhd) Tâm J của đường tròn ngoại tiếp tam giác HIB thuộc một đường cố định
Đọc tiếp
cho (O;R), đường kính AB cố định. Đường thẳng d tiếp xúc với đường tròn tâm O tại B. Đường kính MN thay đổi sao cho MN không vuông góc với AB và M ko trùng với A và B. Các đường thẳng AM và AN cắt đường thẳng d tại C và D. Gọi I là trung điểm của CD, H là giao điểm của AI và MN. Khi đường kính MN quay xung quanh O. Hãy chứng minh:
a) AM.AC không đổi
b) bốn điểm C,M,N,D cùng nằm trên một đường tròn
c) H thuộc một đường cố định
d) Tâm J của đường tròn ngoại tiếp tam giác HIB thuộc một đường cố định
Cho đường tròn ( O) và dây AB cố định, điểm M tuỳ ý thay đổi trên đoạn thẳng AB. Qua A, M dựng đường tròn tâm I tiếp xúc với đường tròn (O) tại A. Quan B, M dựng đường tròn tâm J tiếp xúc với (O) tại B. Hai đường tròn tâm I và tâm J cắt nhau tại điểm thứ hai là N. C/m MN luôn đi qua một điểm cố định.
Trên nữa đường tròn tâm O đường kính AB , lấy điểm M .Vẽ đường tròn tâm M tiếp xúc với AB tại H .Vẽ tiếp tuyến AC và BD của (M) với C và D là hai tiếp điểm.
1.Tìm hai góc so le trong bằng nhau để chứng minh OM//BD ; OM//AC
2.CHứng minh C ,M , D thẳng hàng và đường thẳng CD tiếp xúc với (O)
3.Giả sử CD=2a.TÍnh AC.BD theo a















