Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:
a) \(\sqrt{x^2+6x+9}\) với x < -3;
b) \(\sqrt{y^4+2y^2+1}\).
Những câu hỏi liên quan
Áp dụng quy tắc chia hai căn bậc hai , hãy tính :
\(\frac{\sqrt{8^2}}{\sqrt{4^{5.}}\sqrt{2^3}}\)
cho biểu thức A= \(\sqrt{x^2-6x+19}-\sqrt{x^2-6x+10}=3\)
hãy tính giá trị của biểu thức
A=\(\sqrt{x^2-6x+19}+\sqrt{x^2-6x+10}\)
VẬN DỤNG BÀI BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI
Các biểu thức dưới dấu căn đều dương
Đat \(\sqrt{x^2-6x+19}=a\ge0,\sqrt{x^2-6x+10}=b\ge0\)
Ta có \(a-b=3\)và \(a^2-b^2=9\)
\(\Rightarrow a+b=9\)
Do \(a+b>a-b\) nên \(b>0\)\(\Leftrightarrow a>0\)
Vậy giá trị của biểu thức A = 9
Đúng 0
Bình luận (0)
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 40
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 5
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 52 . 13
52 . 13 = 4 . 13 . 13 = 2 . 13 2 = 2 . 13 = 26
Đúng 0
Bình luận (0)
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 2 . 162
2 . 162 = 2 . 2 . 81 = 2 . 9 2 = 2 . 9 = 18
Đúng 0
Bình luận (0)
(căn bậc hai(x - (2*căn bậc hai(x-1))) + căn bậc hai(x + 2*căn bậc hai(x -1)))/(x -1)
rút gọn biểu thức - giúp mình nhanh nhanh với huhu
1 tháng 12 2021 lúc 18:02
Câu 2: Áp dụng quy tắc dấu ngoặc để rút gọn biểu thức:
a) A = 23 - x - (x - 46) + 2x - 43
b) B = - (4 - 2x) + [ 76 - x - (x + 99)]
\(A=23-x-x+46+2x-43=26\)
\(B=-4+2x+76-x-x-99=-27\)
Đúng 0
Bình luận (1)
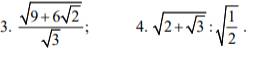áp dụng quy tắc chia căn bậc hai, hãy tính
\(3,\dfrac{\sqrt{9+6\sqrt{2}}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3\left(3+2\sqrt{2}\right)}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3}.\sqrt{3+2\sqrt{2}}}{\sqrt{3}}\)
\(=\sqrt{3+2\sqrt{2}}\)
\(=\sqrt{\sqrt{2^2}+2\sqrt{2}+1}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(=\left|\sqrt{2}+1\right|=\sqrt{2}+1\)
\(4,\sqrt{2+\sqrt{3}}:\sqrt{\dfrac{1}{2}}\)
\(=\sqrt{2+\sqrt{3}}:\dfrac{1}{\sqrt{2}}\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{2}\)
\(=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\sqrt{3^2}+2\sqrt{3}+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)}^2\)
\(=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)
Đúng 3
Bình luận (0)
Áp dụng quy tắc chia hai căn bậc hai, hãy tính: 2300 23