1) Cho MNP cân tại M có MA là đường trung tuyến
C/M : MA là đường phân giác
vẽ hình giúp e vs
Những câu hỏi liên quan
Cho tam giác MNP cân tại M có MA là đường trung tuyến ( A thuộc NP ) gọi G là trọng tâm O là giao điểm của 2 đường trung trực đến cạnh MN và MP.
a/ cm OM=ON=OP
b/ cm 3 điểm ,M,G thẳng hàng
c/ Cho M=13cm,NP=10cm tính MA=,
Cho tam giác MNP cân tại M có MN=10 cm Np= 16 cm và MA là đường cao a) Tính MA và AN b) Chứng minh Ma là tia phân giác của tam giác MNP
Cho tam giác MNP vuông góc tại M, kẻ đường trung tuyến MA. Gọi D là trung điểm của MN, E đối xứng A qua D
a) CMR: E đối xứng A qua MN
b) Tứ giác MENA là hình gì? Vì sao?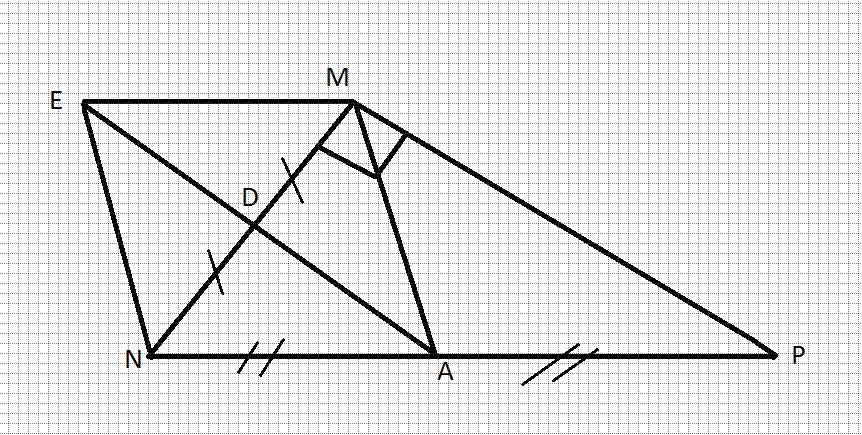
a: Xét ΔMNP có NA/NP=ND/NM
nên DA//MP
=>DA vuông góc với NM
=>EA vuông góc với NM
mà EA cắt NM tại trung điểm của EA
nên E đối xứng A qua MN
b: Xét tứ giác MENA có
D là trung điểm chung của MN và EA
AN=AM
Do đó: MENA là hình thoi
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung diểm của AC. K là điểm đối xướng với M qua điểm Ia) Chứng minh tứ giác AMCK là hình chữ nhậtb) Tứ Giác ABMK là hình gì ? Vì sao ?c) Trên tia đối của tia MA lấy điểm E sao cho ME MA. Chứng minh tứ giác ABEC là hình thoid) Gọi là trung điểm AB, Chứng minh AQIK là hình bình hànhe) QK cắt AI ại N, QC cắt KM tại D. Chứng Minh ND vuông góc Với QIf) EI cắt CM tại P, chứng minh AP đi qua trung điểm cạnh CE và 6MP BC
Đọc tiếp
Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung diểm của AC. K là điểm đối xướng với M qua điểm I
a) Chứng minh tứ giác AMCK là hình chữ nhật
b) Tứ Giác ABMK là hình gì ? Vì sao ?
c) Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh tứ giác ABEC là hình thoi
d) Gọi là trung điểm AB, Chứng minh AQIK là hình bình hành
e) QK cắt AI ại N, QC cắt KM tại D. Chứng Minh ND vuông góc Với QI
f) EI cắt CM tại P, chứng minh AP đi qua trung điểm cạnh CE và 6MP = BC
Từ điểm M ở ngoài đường tròn (O, R) vẽ tiếp tuyến MA đến đường tròn. E là trung điểm MA ; I, H lần lượt là hình chiếu của E và A trên MO. Từ I vẽ tiếp tuyến IK với (O). a) Chứng minh I nằm ngoài đường tròn (O, R) b) Qua M vẽ cát tuyến MBC ( B nằm giữa M và C ). Chứng minh tứ giác BHOC nội tiếp. c) Chứng minh HA là phân giác của góc BHC và tam giác MIK cân Ai giúp mình phần b, c với mình đang cần gấp.
Đọc tiếp
Từ điểm M ở ngoài đường tròn (O, R) vẽ tiếp tuyến MA đến đường tròn. E là trung điểm MA ; I, H lần lượt là hình chiếu của E và A trên MO. Từ I vẽ tiếp tuyến IK với (O).
a) Chứng minh I nằm ngoài đường tròn (O, R)
b) Qua M vẽ cát tuyến MBC ( B nằm giữa M và C ). Chứng minh tứ giác BHOC nội tiếp.
c) Chứng minh HA là phân giác của góc BHC và tam giác MIK cân
Ai giúp mình phần b, c với mình đang cần gấp.
từ điểm M nằm ngoài đường tròn (0),vẽ các tuyến MBC và tiếp tuyến MA vs đường tròn tia phân giác của góc BAC cắt dây BC tại E.
A.chung Minh hệ thức MA^2=MB.MC
B.chung minh tâm giác AME cân .
Giúp mình với.
CHO TAM GIÁC ABC CÂN TẠI
A/ĐƯỜNG PHÂN GIÁC BD,EC (D ∈ AC ,E ∈ AB).CMR TỨ GIÁC BEDC LÀ HÌNH THANG CÂN CÓ CẠNH BÊN BẰNG ĐÁY NHỎ
B/ĐƯỜNG CAO BH,CK (H ∈ AC, K ∈ AB).CMR: BKHC LÀ HÌNH THANG CÂN
C/ĐƯỜNG TRUNG TUYẾN BM ,CN (M ∈ AC, N ∈ AB). CMR :BNCM LÀ HÌNH THANG CÂN
các bạn giúp mik vs...........................................................................................................
a: Xét ΔADB và ΔAEC có
góc BAD chung
AB=AC
góc ABD=góc ACE
Do đó: ΔADB=ΔAEC
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
Xét ΔEDB có góc EDB=góc EBD(=góc DBC)
nên ΔEDB cân tại E
=>BE=ED=DC
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó ΔAHB=ΔAKC
=>AH=AK
Xét ΔABC có AK/AB=AH/AC
nên KH//BC
=>BKHC là hình thang
mà góc KBC=góc HCB
nên BKHC là hình thang cân
c: Xét ΔABC có AN/AB=AM/AC
nên NM//BC
=>BNMC là hình thang
mà góc B=góc C
nên BNMC là hình thang cân
Đúng 0
Bình luận (0)
Bài 5: Cho tam giác MNP cân tại M. Kẻ MK PN (K NP)a) Chứng minh: MNK MPK và MK là đường trung trực của đoạn thẳng NPb) Trên tia đối của tin NP lấy điểm A, trên tia đối của tia PN lấy điểm B sao cho AN BP.Chứng minh: MA MBc) Lấy điểm D bất kỳ trên cạnh MA (D khác A, M). Qua D, kẻ đường thẳng song song với ABcắt MB tại E. Chứng minh: MDE cânAi giải nhanh giúp mk vs mk tick cho
Đọc tiếp
Bài 5: Cho tam giác MNP cân tại M. Kẻ MK PN (K NP)
a) Chứng minh: MNK = MPK và MK là đường trung trực của đoạn thẳng NP
b) Trên tia đối của tin NP lấy điểm A, trên tia đối của tia PN lấy điểm B sao cho AN = BP.
Chứng minh: MA = MB
c) Lấy điểm D bất kỳ trên cạnh MA (D khác A, M). Qua D, kẻ đường thẳng song song với AB
cắt MB tại E. Chứng minh: MDE cân
Ai giải nhanh giúp mk vs mk tick cho
a) Xet tam giac MNK va tam giac MPK co:
Goc MKP = goc MKN = 90 do ( MK vuong goc voi NP ) (1)
MK ( canh chung ) (2)
MN = MP ( tam giac MNP can tai M ) (3)
Tu (1), (2), (3) => Tam giac MNK = tam giac MPK ( canh huyen - canh goc vuong )
b) Ta co: goc MNK = goc MPK ( 2 goc o day cua tam giac can MNP ) va
goc MPK + goc MPB = 180 do ( ke bu ); goc MNK + goc MNA = 180 do ( ke bu )
ma goc MPK = goc MNK ( cmt ) => goc MPB = goc MNA
Xet tam giac MNA va tam giac MPB co:
PB = NA ( gt ) (1)
MP = MN ( tam giac MNP can tai M ) (2)
goc MPB = goc MNA ( cmt ) (3)
Tu (1), (2) ,(3) => tam giac MNA = tam giac MPB ( c.g.c )
=> MA = MB ( 2 canh tuong ung )
c) Ta co: DE // AB ma goc MDE va goc MAB la 2 goc dong vi => goc MDE = goc MAB
MED MBA MED MBA
Vay tam giac MDE la tam giac can ( tam giac MDE co 2 goc bang nhau )
cho hình tròn tâm (o,r) cố định từ điểm M nằm ngoài đường tròn kẻ hai tiếp tuyến MA và MB. Gọi M là giao điểm OM,AB
a, c.minh OM vuông góc AB và OH.OM=R2
b, từ M kẻ các tuyến MNP với đường tròn. Gọi I là trung điểm của NP. Cminh 4 điểm AMOI thuộc 1 đường tròn
giúp em với ạ e đang rất cần e cảm ơnnn^^
△ ABC có đường trung tuyến AM đồng thời là đường phân giác. Trên tia AM lấy điểm D sao cho MD=MA. CMR:
a) AB=CD
b) △ACD cân tại A
c) △ABC cân tại A
(vẽ hình và ghi giả thiết kl)
a: Xét ΔAMB và ΔDMC có
MA=MD
AMB=DMC
MB=MC
Do đó: ΔAMB=ΔDMC
Suy ra: AB=CD
c: Xét ΔABC có
AM là đường trung tuyến ứng với cạnh BC
AM là đường phân giác ứng với cạnh BC
Do đó: ΔABC cân tại A
Đúng 3
Bình luận (2)
