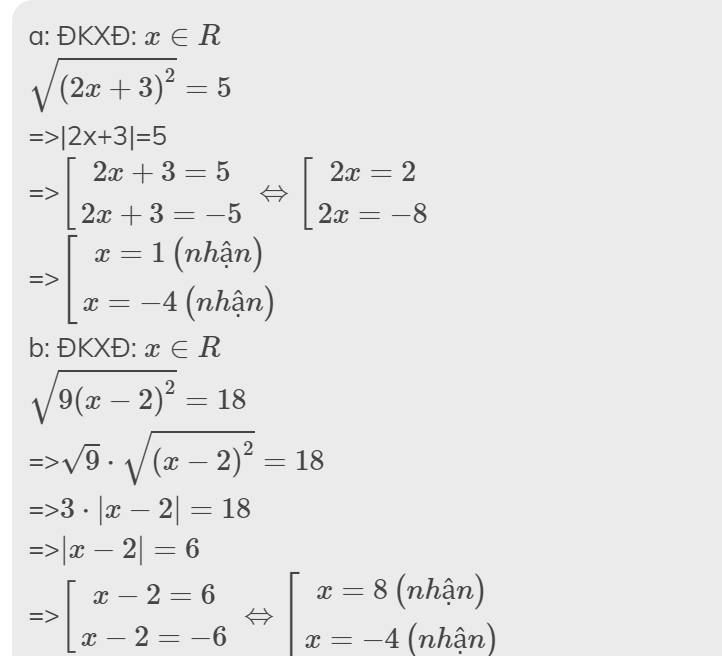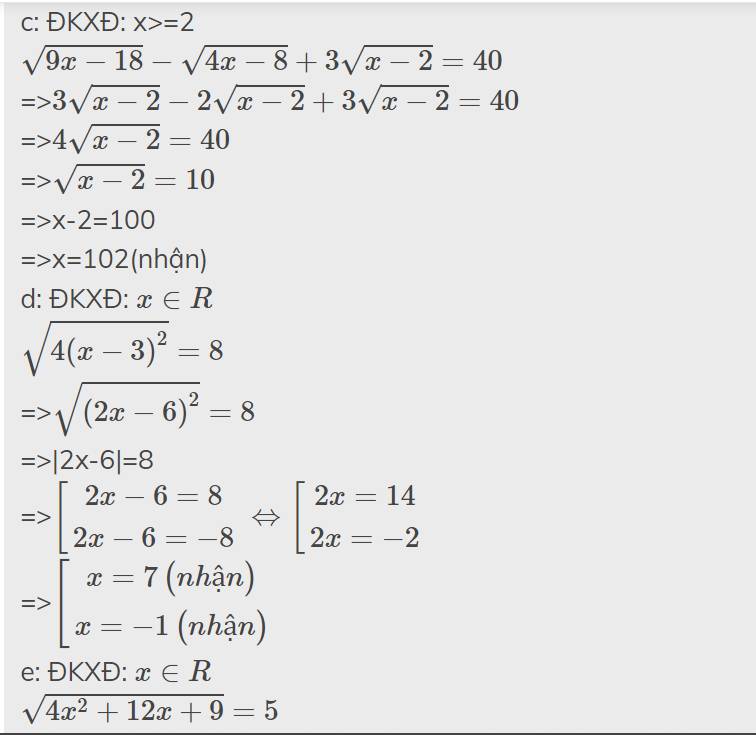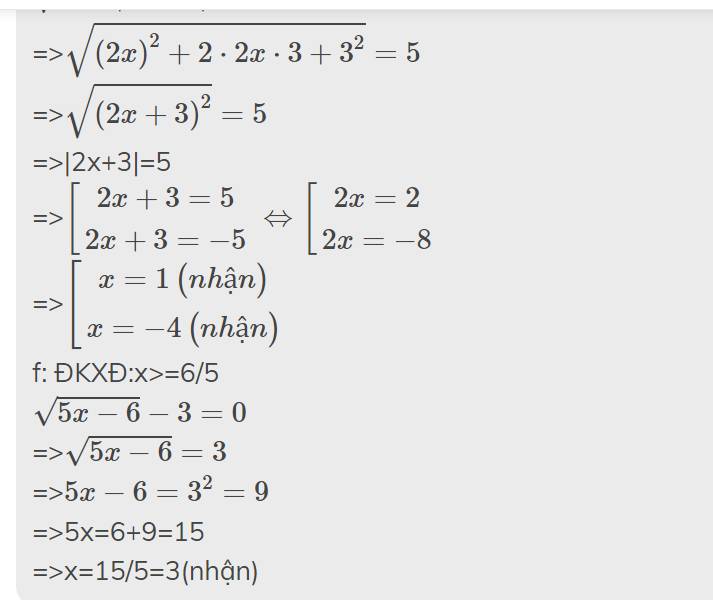Giải phương trình: \(2\sqrt[3]{3x-2}+3\sqrt{6-5x}-8=0\)

Những câu hỏi liên quan
giải phương trình
\(2\sqrt[3]{3x-2}+3\sqrt{6-5x}-8=0\)
giải phương trình sau:
a) \(4x^2+\left(8x-4\right).\sqrt{x}-1=3x+2\sqrt{2x^2+5x-3}\)
b) \(8x^3-36x^2+\left(1-3x\right)\sqrt{3x-2}-3\sqrt{3x-2}+63x-32=0\)
c) \(2\sqrt[3]{3x-2}-3\sqrt{6-5x}+16=0\)
d) \(\sqrt[3]{x+6}-2\sqrt{x-1}=4-x^2\)
giải các phương trình sau:
a \(\sqrt{3x^2-17x+4}=3x-2\)
b \(2x^2-10x-3\sqrt{x^2-5x+4}+6=0\)
a.
\(\Leftrightarrow\left\{{}\begin{matrix}3x-2\ge0\\3x^2-17x+4=\left(3x-2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\3x^2-17x+4=9x^2-12x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\6x^2+5x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\\left[{}\begin{matrix}x=0< \dfrac{2}{3}\left(loại\right)\\x=-\dfrac{5}{6}< \dfrac{2}{3}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
Đúng 1
Bình luận (0)
b.
ĐKXĐ: \(\left[{}\begin{matrix}x\ge4\\x\le1\end{matrix}\right.\)
Đặt \(\sqrt{x^2-5x+4}=t\ge0\Leftrightarrow x^2-5x=t^2-4\)
\(\Rightarrow2x^2-10x=2t^2-8\)
Phương trình trở thành:
\(2t^2-8-3t+6=0\)
\(\Leftrightarrow2t^2-3t-2=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-\dfrac{1}{2}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2-5x+4}=2\)
\(\Leftrightarrow x^2-5x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải phương trình:\(\sqrt{5x^2+x+3}-2\sqrt{5x-1}+x^2-3x+3=0\)
ĐKXĐ:
\(\left(2x+2-2\sqrt{5x-1}\right)+\left(\sqrt{5x^2+x+3}-\left(2x+1\right)\right)+x^2-3x+2=0\)
\(\Leftrightarrow\dfrac{2\left(x^2-3x+2\right)}{x+1+\sqrt{5x-1}}+\dfrac{x^2-3x+2}{\sqrt{5x^2+x+3}+2x+1}+x^2-3x+2=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(\dfrac{2}{x+1+\sqrt{5x-1}}+\dfrac{1}{\sqrt{5x^2+x+3}+2x+1}+1\right)=0\)
\(\Leftrightarrow x^2-3x+2=0\)
Đúng 4
Bình luận (0)
Giải các phương trình sau:1) sqrt{3x^2+5x+8}-sqrt{3x^2+5x+1}12) x^2-2x-12+4sqrt{left(4-xright)left(2+xright)}03) 3sqrt{x}+dfrac{3}{2sqrt{x}}2x+dfrac{1}{2x}-74) sqrt{x}-dfrac{4}{sqrt{x+2}}+sqrt{x+2}05)left(x-7right)sqrt{dfrac{x+3}{x-7}}x+46) 2sqrt{x-4}+sqrt{x-1}sqrt{2x-3}+sqrt{4x-16}7) sqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}dfrac{x+3}{2}Giúp mình với ajk, mink đang cần gấp
Đọc tiếp
Giải các phương trình sau:
1) \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
2) \(x^2-2x-12+4\sqrt{\left(4-x\right)\left(2+x\right)}=0\)
3) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}=2x+\dfrac{1}{2x}-7\)
4) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
5)\(\left(x-7\right)\sqrt{\dfrac{x+3}{x-7}}=x+4\)
6) \(2\sqrt{x-4}+\sqrt{x-1}=\sqrt{2x-3}+\sqrt{4x-16}\)
7) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\dfrac{x+3}{2}\)
Giúp mình với ajk, mink đang cần gấp
Giải phương trình: \(2\sqrt[3]{3x-2}+3\sqrt{6-5x}-8=0\)
\(2\sqrt[3]{3x-2}+3\sqrt{6-5x}-8=0\)
\(\Leftrightarrow\left(2\sqrt[3]{3x-2}+4\right)+\left(3\sqrt{6-5x}-12\right)=0\)
\(\Leftrightarrow2\dfrac{3x-2+8}{\sqrt[3]{\left(3x-2\right)^2}-\sqrt[3]{2\left(3x-2\right)}+\sqrt[3]{4}}+3\dfrac{6-5x-16}{\sqrt{6-5x}+4}=0\)
\(\Leftrightarrow\dfrac{6\left(x+2\right)}{\sqrt[3]{\left(3x-2\right)^2}-\sqrt[3]{2\left(3x-2\right)}+\sqrt[3]{4}}+\dfrac{-15\left(x+2\right)}{\sqrt{6-5x}+4}=0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{6}{\sqrt[3]{\left(3x-2\right)^2}-\sqrt[3]{2\left(3x-2\right)}+\sqrt[3]{4}}+\dfrac{-15}{\sqrt{6-5x}+4}\right)=0\)
\(\Rightarrow x+2=0\Rightarrow x=-2\)
Đúng 0
Bình luận (0)
Giải Phương Trình
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{5x-6}-3=0\)
giải hệ phương trình : \(2\left(2x-1\right)-3\sqrt{5x-6}=\sqrt{3x-8}\)
Giải Phương Trình:
\(2\left(2x-1\right)-3\sqrt{5x-6}=\sqrt{3x-8}.\)