Tìm x, y, f là số nguyên biết :
x2=y+1
y2=f+1
f2=x+1
ai nhanh nhất và đúng mình tick cho
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Đồ thị hàm f(x) như hình vẽ.
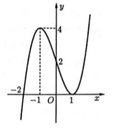
Số đường tiệm cận đứng của đồ thị hàm số y = x 2 - 1 f 2 ( x ) - 4 f ( x ) là
A. 4
B. 1
C. 2
D. 3
là số nguyên tố
1.
\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)
\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)
\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)
\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)
Đặt \(xy=a\Rightarrow0< a\le1\)
\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)
\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)
\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)
\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)
\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)
\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)
Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)
2.
Đặt \(A=9^n+62\)
Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)
Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)
\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)
Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\) và \(6m+1\)
\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)
\(\Leftrightarrow36m^2=9^n+63\)
\(\Leftrightarrow4m^2=9^{n-1}+7\)
\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)
\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)
Pt ước số cơ bản, bạn tự giải tiếp
Viết công thức hàm y = f(x) biết y tỉ lệ thuận vs x theo hệ số tỉ lệ k = 1/4
a) Tìm x để f(x) = -5
b) Chứng tỏ rằng nếu : x1 > x2 => f(x1) > f(x2)
giúp mình với đúng mình dùng 3 acc tick cho
y/x =k=1/4
y= f(x) =x/4
a) y = -5 =x/4 => x = -20
b) t đi, rùi làm tiếp
Tìm các số nguyên x,y biết:
x.(y-3) = -12
Bạn nào làm nhanh và đúng nhất mình sẽ tick cho
x.(y-3) = -12 .
xy-3x=-12
x(y-3)=-1.12=-12.1=-2.6=-6.2=-3.4=-4.3
Xét các TH sau:
x=-1 ;y-3=12
x=-2 ;y-3=6
x=-3 ;y-3=4
x=-4 ;y-3=3
x=-6 ;y-3=2
x=-12 ;y-3=1
x=1 ;y-3=-12
x=2 ;y-3=-6
x=3 ;y-3=-4
x=4 ;y-3=-3
x=6 ;y-3=-2
x=12 ;y-3=-1
tìm 2 số nguyên x,y biết x2+(y-1)2=25
ai làm đúng và nhanh nhất mình tick cho.
cho hàm số y = f(x)=(2m-1)*x
a Tìm m biết đồ thị hàm số đi qua A(1;-3)
b. Tìm m biết f(2)=5
mình đang rất gấp ai làm nhanh đúng mình tick cho .
Tìm các số tự nhiên x,y biết 2xy+x=5y
Tìm các số nguyên tố x y thỏa mãn: 272x=11y+29
Tìm số n có 16 ước , biết n chia hết cho 6 và n chia hết cho 125
Trình bày nhanh nhé! Ai nhanh nhất thì mình tick luôn!( Nhớ là đúng đấy nhé)
Hạn là 10:30
tìm nguyên tố x và y biết x^2-6y^2=1
bận nao f nhanh thì mình tick nhé thanks
\(x^2-6y^2=1\)
\(\rightarrow x^2=6y^2+1\)
\(\rightarrow x^2=\left(2k+1\right)^2=4k^2+4k+1=4k\left(k+1\right)+1\)
Ta thấy \(k\left(k+1\right)\)là tích của hai số nguyên liên tiếp nên \(k\left(k+1\right)⋮2\rightarrow4k\left(k+1\right)⋮8\)
\(\rightarrow6y^2⋮8\rightarrow y^2⋮2\rightarrow y=2\) do \(y\)là số nguyên tố.
\(\rightarrow x=5\)
Vậy \(\left(x;y\right)=\left(5;2\right)\)
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
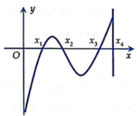
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .