Bài 1
Bài 2
Bài 3 
ĐỀ CHÍNH THỨC :
Tổng quan | Bài 1 | Bài 2 | Bài 3 | Bài 4 |
Tên bài làm | BL1.PAS | BL2.PAS | BL3.PAS | BL4.PAS |
Dữ liệu vào | Nhập từ bàn phím | Nhập từ bàn phím | RECT.INP | FIBO.INP |
Dữ liệu ra | In ra màn hình | In ra màn hình | RECT.OUT | FIBO.OUT |
Giới hạn | 1 giây | 1 giây | 2 giây | 2 giây |
Bài 1:(5 điểm)
Viết chương trình nhập vào từ bàn phím một số N nguyên dương
(1<=N<32767). In ra màn hình các thông tin sau:
a) Số các ước số nguyên dương của số N.
b) Tổng số các ước số nguyên dương của N.
Ví dụ: Nhập từ bàn phím N = 10
In ra màn hình:
Co tat ca 4 uoc so
Tong cac uoc la 18
Bài 2:(5 điểm)
Nhập từ bàn phím một xâu kí tự S và một kí tự K.
Hãy in ra màn hình số lượng kí tự K có trong xâu kí tự S và các vị trí xuất hiện của kí tự K trong xâu S. Nếu không có kí tự K trong xâu S thì in ra màn hình dòng thông báo:
Khong co
Ví dụ:
Xâu kí tự S và kí tự K nhập từ bàn phím | In ra màn hình |
KITHITINHOCTRETHANHPHO T | 4 3 6 12 15 |
SOGIAODUC M | Khong co |
Bài 3: RECTANGLE (7,5 điểm)
Trên giấy kẻ ô khổ N x N có vẽ một số hình chữ nhật. Mỗi hình chữ nhật được tạo ra từ các ô nguyên vẹn, các hình chữ nhật khác nhau không chồng lên nhau và không tiếp xúc nhau (Ví dụ : Hình vẽ dưới đây có 4 hình chữ nhật).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cho mảng A có kích thước N x N, trong đó A[i,j]=1 nếu ô [i,j] thuộc một hình chữ nhật nào đó, còn A[i,j] =0 trong trường hợp ngược lại.
Hãy viết chương trình xác định số các hình chữ nhật có trong bảng.
Dữ liệu vào: Từ File văn bản RECT.INP có cấu trúc như sau:
- Dòng đầu tiên ghi số nguyên dương N (N<=250).
- N dòng tiếp theo mỗi dòng ghi N số 0 hoặc 1 là các phần tử của mảng, mỗi số viết cách nhau ít nhất một dấu cách.
Dữ liệu ra: Ghi ra File văn bản RECT.OUT gồm duy nhất một số là số hình chữ nhật tìm được.
Ví dụ:
RECT.INP | RECT.OUT |
4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 |
7 1 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 | 4 |
Bài 4: FIBONACCI (7,5 điểm)
Dãy số Fibonacci được định nghĩa như sau:
U1 = U2 = 1; Un+1 = Un + Un-1 (với mọi số nguyên dương n, n > 1).
Như vậy, dãy số Fibonacci có dạng sau: 1, 1, 2, 3, 5, 8, 13, 21, 34,…
Với một số tự nhiên x bất kỳ khác 0 ta có thể phân tích thành tổng các số Fibonacci khác nhau (số số hạng của tổng có thể là từ 1 trở lên). Chẳng hạn x = 9, khi đó, ta có:
9 = 1 + 8 hoặc 9 = 1 + 3 + 5
Trong hai cách phân tích trên thì cách thứ hai có số số hạng nhiều nhất (3 số hạng).
Yêu cầu: Cho trước một số nguyên dương x (x <= 10000). Hãy cho biết, nếu biểu diễn x thành tổng của các số Fibonacci khác nhau thì số số hạng nhiều nhất của một tổng là bao nhiêu?
Dữ liệu vào: Cho trong file văn bản FIBO.INP chỉ ghi một số nguyên dương x (x<=10000).
Dữ liệu ra: Ghi ra file văn bản FIBO.OUT gồm một số nguyên dương n duy nhất là số số hạng của tổng có số số hạng nhiều nhất trong các tổng.
Ví dụ:
FIBO.INP | FIBO.OUT |
9 | 3 |
Chú ý: Đề thi gồm có 2 trang - Giám thị coi thi không được giải thích gì thêm
ĐÁP ÁN PHẦN LẬP TRÌNH
Bài 1:( 5 điểm) (Có 5 Test ứng với 5 giá trị của N, đúng mỗi Test cho 1 điểm. Không yêu cầu chính xác các từ trong câu trả lời , chủ yếu đúng số ước và tổng số các ước)
Nhập N vào từ bàn phím :
Stt | N | Kết quả trên màn hình |
1 | 10 | Co tat ca 4 uoc so Tong cac uoc la 18 |
2 | 50 | Co tat ca 6 uoc so Tong cac uoc la 93 |
3 | 707 | Co tat ca 4 uoc so Tong cac uoc la 816 |
4 | 5005 | Co tat ca 16 uoc so Tong cac uoc la 8064 |
5 | 32766 | Co tat ca 16 uoc so Tong cac uoc la 67584 |
Bài 2:( 5 điểm)
Có 5 bộ TEST chạy đúng mỗi bộ cho 1 điểm
Stt | Xâu kí tự S và kí tự K | In ra màn hình |
1 | KITHITINHOCTRETHANHPHO T | 4 3 6 12 15 |
2 | SOGIAODUC M | Khong co |
3 | NGONGUPASCAL A | 2 8 11 |
4 | BANADANANG N | 3 3 7 9 |
5 | HOIANMYSON O | 2 2 9 |
Bài 3:( 7,5 điểm)
Có 6 bộ TEST : 3 Test đầu chạy đúng mỗi bộ cho 1,5 điểm,3 Test cuối chạy đúng mỗi bộ cho 1 điểm
Stt | RECT.INP | RECT.OUT |
1 | 3 1 0 0 0 0 0 1 1 1 | 2 |
2 | 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 |
3 | 7 1 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 | 4 |
4 | 15 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 | 6 |
5 | Nội dung như File RECT5.INP | 20 |
6 | Nội dung như File RECT6.INP | 125 |
Bài 4:( 7,5 điểm)
Có 5 bộ TEST: Chạy đúng mỗi bộ cho 1,5 điểm.
Stt | FIBO.INP | FIBO.OUT |
1 | 9 | 3 |
2 | 50 | 6 |
3 | 100 | 7 |
4 | 6763 | 17 |
5 | 9989 | 13 |
Bài 1.Tìm số nguyên n sao cho n+6 chia hết cho n+2
Bài 2. Tìm số nguyên n sao cho 3n+2 chia hết cho n+1
Bài 3. Tìm số nguyên x biết (x-2).(x+3)<0
Bài 4. Tìm số nguyên x biết (4-2x).(x+3)>0
Bài 1: cho A = 1 + 21 + 22 + 23 + ...... + 22007
a)Tính 2.A
b)Chứng minh A = 22006 - 1
Bài 2: cho A = 1 + 3 + 31 + 32 + 33 + 34 + 35 + 36 + 37
a)Tính 2.A
b)Chứng minh A = (38 - 1) : 2
Bài 3: cho B = 1 + 3 + 32 + ..... + 32006
a)Tính 3.B
b)Chứng minh B = (32007 - 1) : 2
Bài 4: cho C = 1 + 4 + 42 + 43 + 45 + 46
a)Tính 4.C
b)Chứng minh C = (47 - 1) : 3
Bài 5: Tính tổng
S = 1+ 2+ 22+ 23 + ...... + 22017
1.
a.\(A=1+2^1+2^2+2^3+...+2^{2007}\)
\(2A=2+2^2+2^3+....+2^{2008}\)
b. \(A=\left(2+2^2+2^3+...+2^{2008}\right)-\left(1+2^1+2^2+..+2^{2007}\right)\)
\(=2^{2008}-1\) (bạn xem lại đề)
2.
\(A=1+3+3^1+3^2+...+3^7\)
a. \(2A=2+2.3+2.3^2+...+2.3^7\)
b.\(3A=3+3^2+3^3+...+3^8\)
\(2A=3^8-1\)
\(=>A=\dfrac{2^8-1}{2}\)
3
.\(B=1+3+3^2+..+3^{2006}\)
a. \(3B=3+3^2+3^3+...+3^{2007}\)
b. \(3B-B=2^{2007}-1\)
\(B=\dfrac{2^{2007}-1}{2}\)
4.
Sửa: \(C=1+4+4^2+4^3+4^4+4^5+4^6\)
a.\(4C=4+4^2+4^3+4^4+4^5+4^6+4^7\)
b.\(4C-C=4^7-1\)
\(C=\dfrac{4^7-1}{3}\)
5.
\(S=1+2+2^2+2^3+...+2^{2017}\)
\(2S=2+2^2+2^3+2^4+...+2^{2018}\)
\(S=2^{2018}-1\)
4:
a:Sửa đề: C=1+4+4^2+4^3+4^4+4^5+4^6
=>4*C=4+4^2+...+4^7
b: 4*C=4+4^2+...+4^7
C=1+4+...+4^6
=>3C=4^7-1
=>\(C=\dfrac{4^7-1}{3}\)
5:
2S=2+2^2+2^3+...+2^2018
=>2S-S=2^2018-1
=>S=2^2018-1
bài 1
bài 2

bài 3
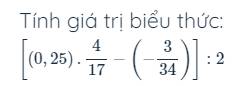
bài 4
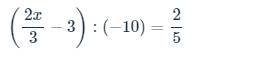
bài 5
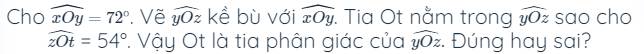
bài 6
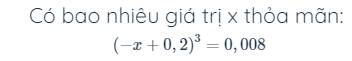
bài 7
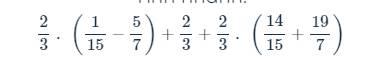
bài 8

bài 9
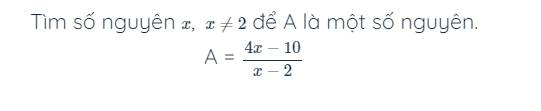
gấp ạ !!! , nhanh tick cho ạ
Bài 9:
Để A là số nguyên thì \(4x-10⋮x-2\)
=>\(4x-8-2⋮x-2\)
=>\(-2⋮x-2\)
=>\(x-2\inƯ\left(-2\right)\)
=>\(x-2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{3;1;4;0\right\}\)
Bài 8:
Diện tích mảnh vườn là:
\(\dfrac{1}{2}\cdot10\cdot\left(15+25\right)=5\cdot40=200\left(m^2\right)\)
Khối lượng thóc thu được là:
\(200:1\cdot0,7=140\left(kg\right)\)
Bài 7:
\(\dfrac{2}{3}\cdot\left(\dfrac{1}{15}-\dfrac{5}{7}\right)+\dfrac{2}{3}+\dfrac{2}{3}\cdot\left(\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{1}{15}-\dfrac{5}{7}+1+\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(1+1+2\right)\)
\(=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\)
Bài 6:
\(\left(-x+0,2\right)^3=0,008\)
=>\(-x+0,2=\sqrt[3]{0,008}=0,2\)
=>-x=0
=>x=0
=>Có 1 giá trị x thỏa mãn
Câu 4:
\(\left(\dfrac{2x}{3}-3\right):\left(-10\right)=\dfrac{2}{5}\)
=>\(x\cdot\dfrac{2}{3}-3=\dfrac{2}{5}\cdot\left(-10\right)=-4\)
=>\(x\cdot\dfrac{2}{3}=-4+3=-1\)
=>\(x=-1:\dfrac{2}{3}=-\dfrac{3}{2}\)
Bài 1: Tìm x, biết 4 – 2(x + 1) = 2
Bài 2. Tìm x biết: |2x – 3| - 1 = 2
Bài 3. Tìm x, biết: 3 1 3 x + 16 3 4 = - 13,25
Bài 4: Tìm x biết: 60% x + 2 3 x = - 76
Bài 5: Tìm x, biết: a) 11 - (-53 + x) = 97 b) -(x + 84) + 213 = -16
thanks
Bài 1:
Ta có: \(4-2\left(x+1\right)=2\)
\(\Leftrightarrow2\left(x+1\right)=2\)
\(\Leftrightarrow x+1=1\)
hay x=0
Bài 2:
Ta có: \(\left|2x-3\right|-1=2\)
\(\Leftrightarrow\left|2x-3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
Bài 1.
Bài 2
bài 3
giúp đi rồi mình tick cho
Bài 3:
Bác An có:
24:4/7=42(con)
Bác An đã bán đi:
42x3/7=18(con)
Bài 4: Sao tìm được n khi chỉ cho 1 vế
Bài 6:
\(\left(2x-3\right)^2=\dfrac{196}{225}=\left(\dfrac{14}{15}\right)^2=\left(-\dfrac{14}{15}\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=\dfrac{14}{15}\\2x-3=-\dfrac{14}{15}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{14}{15}+3=\dfrac{59}{15}\\2x=\dfrac{-14}{15}+3=-\dfrac{31}{15}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{59}{15}:2=\dfrac{59}{30}\\x=-\dfrac{31}{15}:2=-\dfrac{31}{30}\end{matrix}\right.\)
Bài 1

Bài 2 Cho Hình vẽ sau: 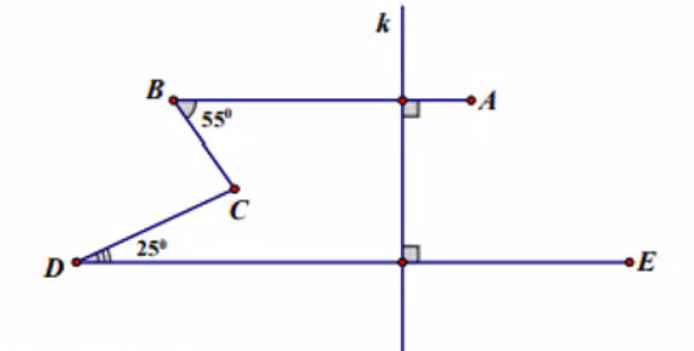

Bài 1: Dạng 1
a.
3/2và4/7
3/5;4/3và1/2
Bài 2: Dạng 2
a.
3/14và4/7
3/5;4/3và1/15
Bài 3: Dạng 3
a.
3/9và4/12
3/12;4/16và1/8
giúp mk với mk đang cần gấp
ai xong đầu tiên thì mk sẽ tick cho người đó
Bài 3:
a: 3/9=1/3=4/12
b: 3/12=1/4=4/16
mà 1/4>1/8
nên 3/12=4/16>1/8
bài 1 bài 2
bài 2 giúp mik hai bài này với (kẻ bảng nx nha ) cảm ưn nhiều
giúp mik hai bài này với (kẻ bảng nx nha ) cảm ưn nhiều![]()
Bài 2:
Gọi khối lượng thóc năm ngoái đơn vị thứ nhất thu hoạch được là x(tấn), đơn vị thứ hai thu hoạch được là y(tấn)
(Điều kiện: x>0 và y>0)
Sản lượng thóc năm nay của đơn vị thứ nhất là: \(x\left(100\%+15\%\right)=1,15x\left(tấn\right)\)
Sản lượng thóc năm nay của đơn vị thứ hai là:
\(y\left(1+12\%\right)=1,12y\left(tấn\right)\)
Tổng sản lượng thóc năm ngoái của hai đơn vị là 720 tấn nên x+y=720(1)
Tổng sản lượng thóc của hai đơn vị năm nay là 819 tấn nên 1,15x+1,12y=819(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=720\\1,15x+1,12y=819\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1,15x+1,15y=828\\1,15x+1,12y=819\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0,03y=9\\x+y=720\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=300\\x=420\end{matrix}\right.\left(nhận\right)\)
Vậy: Sản lượng thóc năm ngoái của đơn vị thứ nhất là 420 tấn
Sản lượng thóc năm ngoái của đơn vị thứ hai là 300 tấn
Sản lượng thóc năm nay của đơn vị thứ nhất là 420*1,15=483 tấn
Sản lượng thóc năm nay của đơn vị thứ hai là:
300*1,12=336 tấn