Tìm số tự nhiên n lớn nhất sao cho n2 là ước của 10! Biết a! = 1 . 2 . 3 . 4 . ... . a .

Những câu hỏi liên quan
Giải các bài toán sau:1. Ước nguyên tố lớn nhất của:36893 + 947877722. Tìm số tự nhiên n nhỏ nhất, biết rằng:Ước chung lớn nhất của (1885n + 5) và (23503n +9) 20113. Tìm số tự nhiên n lớn nhất sao cho 2013 : n, R3 và 20122013 : n, R 234. Cho A frac{28n^2+3n+2015}{2n-3} (ninN). Tìm n nhỏ nhất để A chia hết 87
Đọc tiếp
Giải các bài toán sau:
1. Ước nguyên tố lớn nhất của:
36893 + 94787772
2. Tìm số tự nhiên n nhỏ nhất, biết rằng:
Ước chung lớn nhất của (1885n + 5) và (23503n +9) =2011
3. Tìm số tự nhiên n lớn nhất sao cho 2013 : n, R=3 và 20122013 : n, R = 23
4. Cho A = \(\frac{28n^2+3n+2015}{2n-3}\) (n\(\in\)N). Tìm n nhỏ nhất để A chia hết 87
Cho a=20! (Biết n!=1.2.3...n).
a) Tìm ước lớn nhất của a là lập phương của một số tự nhiên.
b) Tìm ước lớn nhất của a là bình phương của một số tự nhiên.
a) Tìm các số tự nhiên n sao cho 6 ⁝ (n+1).
b) Biết hai số 23.3a và 2b.35 có ước chung lớn nhất là 22.35 và bội chung nhỏ nhất là 23.36. Hãy tìm giá trị của các số tự nhiên a và b.
a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
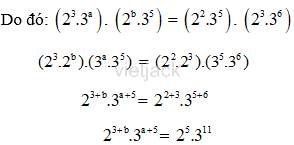
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Đúng 5
Bình luận (0)
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6
Đúng 0
Bình luận (0)
a) Tìm các số tự nhiên n sao cho 6 ⁝ (n+1).
b) Biết hai số 23.3a và 2b.35 có ước chung lớn nhất là 22.35 và bội chung nhỏ nhất là 23.36. Hãy tìm giá trị của các số tự nhiên a và b.
a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
Đúng 1
Bình luận (1)
a) Tìm các số tự nhiên n sao cho 6 ⁝ (n+1).
b) Biết hai số 23.3a và 2b.35 có ước chung lớn nhất là 22.35 và bội chung nhỏ nhất là 23.36. Hãy tìm giá trị của các số tự nhiên a và b.
a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
Đúng 2
Bình luận (0)
Bài 1. Tìm số tự nhiên a nhỏ nhất để a : 7 dư 4; a : 9 dư 5 và a : 15 dư 8.
Bài 2. a) Tìm số tự nhiên n để 16 – 3n là ước của 2n + 1.
b) Tìm số tự nhiên n để n2 + 6n là số nguyên tố.
Bài 3. a) Tìm số nguyên tố p sao cho p + 2; p + 6; p + 8; p + 12; p + 14 cũng là số nguyên tố
b) Tìm số tự nhiên n để các số sau nguyên tố cùng nhau: 4n – 3 và 6n + 1
cho bao nhiêu hộp, mỗi hộp có bao nhiêu viên bi? Biết số hộp lớn hơn 6 và nhỏ hơn 30 Bài 5. Tìm số tự nhiên n để: a) n 4 là bội của n. b) n1 là ước của n 5. c) 2 2 n là bội của n3. d*) 2 –1 n là ước của 3 2. n Bài 6. Tìm số tự nhiên n để a) 17.n là số nguyên tố. b) n n 2 . 4 là số nguyên t cần gấp
Câu 1: Cho N36 x 57. Số ước nguyên của N là:…?Câu 2: Số tự nhiên nhỏ nhất có 5 chữ số khác nhau mà tổng bằng 23Câu 3: Cho số M 26x3x5 . Ước nguyên âm nhỏ nhất của M là …?Câu 4: Số tự nhiên n có 3 chữ số lớn nhất sao cho 2n+7 chia hết cho 13Câu 5: Tìm x biết: I x2- 2I + I 2-x2I 28. Tìm tập hợp các gtrị x nguyên thỏa mãn: {…}Câu 6: Số các cặp (x; y) nguyên thỏa mãn biết: xy và x/9 7/y là….Câu 7: Tìm số tự nhiên a bé nhất biết a: 120 dư 58 và a: 135 dư 88Câu 8: Biết a+b 12.Tính A 15a+ 7...
Đọc tiếp
Câu 1: Cho N=36 x 57. Số ước nguyên của N là:…?
Câu 2: Số tự nhiên nhỏ nhất có 5 chữ số khác nhau mà tổng bằng 23
Câu 3: Cho số M= 26x3x5 . Ước nguyên âm nhỏ nhất của M là …?
Câu 4: Số tự nhiên n có 3 chữ số lớn nhất sao cho 2n+7 chia hết cho 13
Câu 5: Tìm x biết: I x2- 2I + I 2-x2I= 28. Tìm tập hợp các gtrị x nguyên thỏa mãn: {…}
Câu 6: Số các cặp (x; y) nguyên thỏa mãn biết: x>y và x/9= 7/y là….
Câu 7: Tìm số tự nhiên a bé nhất biết a: 120 dư 58 và a: 135 dư 88
Câu 8: Biết a+b= 12.
Tính A= 15a+ 7b- (6a-2b)+32
Câu 9: Tổng 30 số tự nhiên liên tiếp là 2025. Giả sử d là ƯCLN của số đó. Khi đó gtrị lớn nhất của d là bao nhiêu.
Câu 10: Cho số tự nhiên B= ax by trong đó a và b là các số tự nhiên khác nhau và khác 0. Biết B2 có 15 ước. Hỏi B3 có tât cả bao nhiêu ước ?
Bài 3. 1) Tim hai số tự nhiên a và b biết rằng a + b 810 và ước chung lớn nhất của chúng bằng 45. 2) Tìm hai số nguyên tố p và q biết rằng pq sao cho p+q và p −g đều là các số nguyên tố. Bài 4. 1) Cho hai số tự nhiên a và b thỏa mãn số m(16a+17b)(17a+16b) là một bội số của 11. Chứng minh rằng số m cũng là một bội số của 121. 2) Tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5 Bài 5. Cho hình vuôn...
Đọc tiếp
Bài 3. 1) Tim hai số tự nhiên a và b biết rằng a + b = 810 và ước chung lớn nhất của chúng bằng 45. 2) Tìm hai số nguyên tố p và q biết rằng p>q sao cho p+q và p −g đều là các số nguyên tố. Bài 4. 1) Cho hai số tự nhiên a và b thỏa mãn số m=(16a+17b)(17a+16b) là một bội số của 11. Chứng minh rằng số m cũng là một bội số của 121. 2) Tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5 Bài 5. Cho hình vuông ABCD. Phần diện tích chung của ABCD và tam giác EFG được tô đen. Diện tích phần tô đen bằng 4/5 diện tích tam giác EFG và bằng 12 diện tích của hình vuông ABCD. Nếu diện tích tam giác EFG bằng 40cm, tính độ dài cạnh của hình vuông ABCD















