cho tam giác ABC cân tại A có AB=AC=a, BC=b. Lấy M về phía C thuộc BC. Tia Md cắt AC tại N, AB tại P. CHứng minh: \(\frac{BM}{BP}-\frac{CM}{CN}\) khi Md di chuyển

Những câu hỏi liên quan
Cho tam giác ABC có AB < AC. kẻ đường phân giác AD của góc BAC( D thuộc BC). Trên cạnh AC lấy điểm M sao cho: AM = AB.
Chứng minh:
a, Tam giác ADB= tam giác ADM.
b, Tia MD cắt tia AB tại điểm N. Chứng minh: BN= CM.
c, AD cắt BM tại H và cắt CN tại K. Chứng minh: BM // CN.
a: Xét ΔABD và ΔAMD có
AB=AM
góc BAD=góc MAD
AD chung
Do đó; ΔABD=ΔAMD
b: Xét ΔDBN và ΔDMC có
góc DBN=góc DMC
DB=DM
góc BDN=góc MDC
Do đó; ΔDBN=ΔDMC
=>BN=MC
c: Xét ΔANC có AB/BN=AM/MC
nên BM//CN
Đúng 1
Bình luận (0)
Cho △△ABC vuông tại A, ˆB�^ 60 độ. a) Tìm góc ˆC�^ và so sánh ba cạnh của △△ABC. b) Tia phân giác của góc ABC cắt AC tại D , lấy điểm M thuộc cạnh BC sao cho AB BM. Chứng minh △△ADB △△MDB c) MD cắt AB tại N. Chứng minh AM// CN
Đọc tiếp
Cho ABC vuông tại A, = 60 độ. a) Tìm góc và so sánh ba cạnh của ABC. b) Tia phân giác của góc ABC cắt AC tại D , lấy điểm M thuộc cạnh BC sao cho AB = BM. Chứng minh ADB = MDB c) MD cắt AB tại N. Chứng minh AM// CN
`@` `\text {dnammv}`
`a,`
Xét `\Delta ABC:`
\(\widehat {A}+ \widehat {B}+ \widehat {C}=180^0 (\text {định lý tổng 3 góc trong 1} \Delta)\)
`90^0+ 60^0 + \hat {B}=180^0`
`-> \hat {B}=180^0-90^0-60^0=30^0`
`->`\(\widehat {A}> \widehat {B} > \widehat {C} (90^0>60^0>30^0)\)
`@` Theo định lý giữa góc và cạnh đối diện trong tam giác:
`-> \text {BC > AC > AB}`
`b,`
Xét `\Delta ABD` và `\Delta MBD`:
`\text {BD chung}`
\(\widehat {ABD}= \widehat {MBD}\) `(\text {tia phân giác}` `\hat {ABC})`
`AB = BC (g``t)`
`=> \Delta ABD = \Delta MBD (c-g-c)`
`c,` Vì `\Delta ABD = \Delta MBD (b)`
`-> \text {DA = DM (2 cạnh tương ứng)}`
`->` \(\widehat {BAD}= \widehat {BMD}\)`=90^0 (\text {2 góc tương ứng})`
Xét `\Delta ADN` và `\Delta MDC`:
`\text {DA = DM (CMT)}`
\(\widehat {ADN} = \widehat {MDC}\) `(\text {đối đỉnh})`
\(\widehat {BAD}= \widehat {BMD}\)`=90^0 (CMT)`
`=> \Delta ADN = \Delta MDC (cgv-gn)`
`-> \text {AN = MC (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{BA = BM (gt)}\\\text{AN = MC (CMT)}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{BN = BA+AN}\\\text{BC = BM+MC}\end{matrix}\right.\)
`=> \text {BN = BC}`
Xét `\Delta BAM:`
`\text {BA = BM}`
`-> \Delta BAM` cân tại `B`
`->`\(\widehat {BAM}= \widehat {BMA}=\)\(\dfrac{180^0-\widehat{B}}{2}\) `(1)`
Xét `\Delta BNC`:
`\text {BN = BC (CMT)}`
`-> \Delta BNC` cân tại `B`
`->`\(\widehat {BNC} = \widehat {BCN}=\)\(\dfrac{180-\widehat{B}}{2}\) `(2)`
Từ `(1)` và `(2)`
`->`\(\widehat {BNC}= \widehat {BAM}\)
Mà `2` góc này nằm ở bị trí đồng vị
`-> \text {AM // NC (tính chất 2 đường thẳng //)}`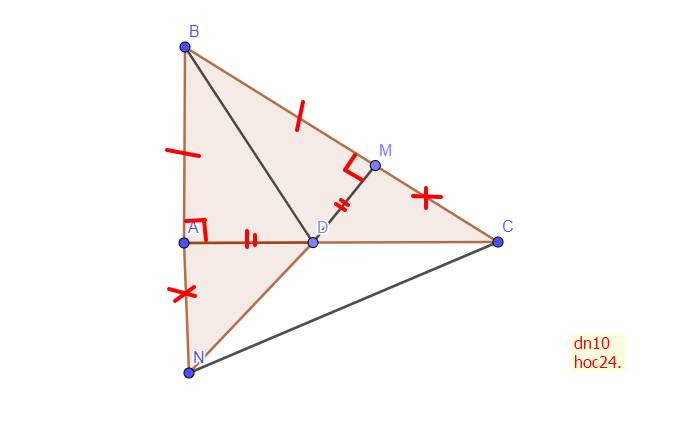
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB < AC).Tia phân giác của B cắt AC tại M.
Kẻ MD vuông góc với BC tại D.
a) Chứng minh tam giác BAD cân.
b) Chứng minh BM là đường trung trực của đoạn thẳng AD.
c) Kéo dài AB và MD cắt ngau tại E. Chứng minh tam giác MEC cân .
d) Chứng minh AD // EC.
Cho tam giác ABC vuông tại A ( AB < AC).Tia phân giác của B cắt AC tại M.
Kẻ MD vuông góc với BC tại D.
a) Chứng minh tam giác BAD cân.
b) Chứng minh BM là đường trung trực của đoạn thẳng AD.
c) Kéo dài AB và MD cắt ngau tại E. Chứng minh tam giác MEC cân .
d) Chứng minh AD // EC.
Cho tam giác ABC ( AB<ÁC ), đường phân giác AM ( M thuộc BC ). Trên cạnh AC lấy điểm D/ AD=AB. Tia AB cắt DM tại E. Chứng minh
a, MB=MD
b,Tam giác MEC cân
c,BM > MC
xét tam giác AMB và AMD , có:
AM:chung
DAM=MAB
AD=AB(gt)
=> tam giác AMB = AMD (C.G.C.)
=> MB=MD
Đúng 0
Bình luận (0)
a) Xét \(\Delta AMB\)và \(\Delta AMD\)có :
AM ( cạnh chung )
\(\widehat{BAM}=\widehat{DAM}\)( gt )
AB = AD ( gt )
Suy ra : \(\Delta AMB\)= \(\Delta AMD\)( c.g.c )
\(\Rightarrow BM=MD\); \(\widehat{ABM}=\widehat{ADM}\)
b) vì \(\widehat{ABM}=\widehat{ADM}\)\(\Rightarrow\widehat{MBE}=\widehat{MDC}\)( cùng bù với hai góc bằng nhau )
Xét \(\Delta BME\)và \(\Delta DMC\)có :
\(\widehat{MBE}=\widehat{MDC}\)( cmt )
BM = DM ( cmt )
\(\widehat{BME}=\widehat{CMD}\)( hai góc đối đỉnh )
Suy ra : \(\Delta BME\)= \(\Delta DMC\)( g.c.g )
\(\Rightarrow\)ME = MC
\(\Rightarrow\)\(\Delta MEC\)cân tại M
c) Ta có : \(\widehat{EBC}=\widehat{BAC}+\widehat{ACB}\)nên \(\widehat{EBC}>\widehat{ACB}\)
hay \(\widehat{MDC}>\widehat{ACB}\)\(\Rightarrow\)MD < MC
Suy ra : MB < MC
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A . AB=3cm , AC=4cm . AM là trung tuyến của tam giác ( M thuộc B ) , trên tia MA lấy D sao cho AM=MD .
a) tính BC
b) chúng minh AB=CD , AB//MD
c) gọi H là trung điểm BM , trên đường thẳng AH lấy E sao cho AH = HE , CE cắt AD tại E . chứng minh EM đi qua chung điểm AC
Cho tam giác ABC có AB = 4 cm, AC = 3 cm, BC = 5 cm.
a) Chứng minh : tam giác ABC vuông
b) Trên AB lấy D sao cho AD = 3 cm. Chứng minh góc ACD = góc ADC
c) Tia phân giác góc CAD cắt BC tại M. So sánh MC và MD ?
d) Cho AM cắt CD tại K. Chứng minh AK < \(\frac{CB}{2}\)
Cho tam giác ABC cân tại A có BC<AB. đường trung tực của AC cắt đường thẳng BC tại M. trên tia đối của tia AM lấy điểm N sao cho AN = BM
a, chứng minh góc AMC= góc BAC
b, chúng minh: CM=CN
c, muốn cho CM vuông góc CN thì tam giác cân ABC cần thêm điểu kiện gì ?
a)MH là đường trung trực đoạn AC cũng là đường trung trực tam giác MAC hạ từ đỉnh M
Suy ra tam giác MAC cân tại M
Suy ra góc MAC = 1800 - 2* góc ACB = góc BAC (đpcm)
b)Tam giác MAC cân tại M suy ra góc MAC = góc MCA= góc ABC
lại có góc MAC + góc CAN= góc ABC+ góc ABM (cùng bằng 1800)
suy ra góc ABM= góc CAN
Xét tam giác AMB và tam giác CNA có
AC=AB (tam giác ABC cân tại A)
MB=AN (gt)
góc ABM= góc CAN(cmt)
Suy ra \(\Delta AMB~\Delta CNA\)(c.g.c)
suy ra góc CMA= góc CNA
suy ra tam giác MCN cân tại C
suy ra MC=CN (đpcm)
c) Có \(CM\perp CN\) và tam giác MCN cân tại C
Suy ra tam giác MCN vuông cân tại C
suy ra góc CNM= góc CMN = 450
mà góc NMA= góc CAB (cmt)
suy ra góc BAC = 450
Vậy để \(CM\perp CN\) thì tam giác ABC cân có góc A = 450
Đúng 3
Bình luận (0)
cho tam giác ABC cân tại A có BC<AB. Đường trung trực của AC cắt đường thẳng BC tại M. Trên tia đối của tia AM lấy điểm N sao cho AN=BM.
a, Chứng minh rằng: góc AMC= góc BAC
b, Chứng minh rằng: CM=CN
c, muốn cho CM vuông góc CN thì tam giác cân ABC phải có thêm điều kiện gì ?
















