Tam giác ABC có AM là trung tuyến, G là trọng tâm biết AM=9cm
a)Tính AG, GM
b)Trên tia đối của tia MA lấy điểm G' sao cho MG'=MG. Lấy I thuộc BC sao cho CI=\(\dfrac{1}{3}\)CB. Chứng minh I là trọng tâm tam giác CGG'

Những câu hỏi liên quan
Cho tam giác ABC,trung tuyến AM và trọng tâm G.Trên tia đối của tia BC lấy điểm E,trên tia đối của tia BC lấy điểm E,trên tia đối của tia CB lấy điểm F sao cho BE=CF
a)chứng minh G là trọng tâm tam giác AEF
b)Gọi N là trung điểm của AF.chứng minh ba điểm E,G,N thẳng hàng
c)Gọi H là trung điểm của G,A,I là trung điểm của GE.Chứng minh IH song song với MN và IH=MN
a: BM+BE=ME
MC+CF=MF
mà BM=MC và BE=CF
nên ME=MF
Xét ΔAEF có
AM là trung tuyến
AG=2/3AM
=>G là trọng tâm
b: Xét ΔAEF có
EN là trung tuyến
G là trọng tâm
=>E,G,N thẳng hàng
c: Xét ΔGAE có GH/GA=GI/GE
nên IH//AE và IH=1/2AE
=>IH//MN và IH=MN
Đúng 0
Bình luận (0)
Cho tam giác ABC đường trung tuyến AM và trọng tâm G. Trên tia đối của tia MA lấy các điểm I và K sao cho MI = MG, IK = IG. Gọi N là trung điểm của CK. Chứng minh rằng ba điểm B, I, N thẳng hàng.
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE CF.a) Chứng minh G là trọng tâm tam giác AEF.b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH MN.
Đọc tiếp
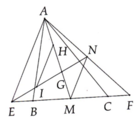
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF.
a) Chứng minh G là trọng tâm tam giác AEF.
b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.
c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH = MN.
Bài 1:Cho tam giác ABC, trung tuyến AM, trọng tâm G. I, K thuộc tia đối AM sao cho MIMG, IKIG. N là tủng điểm của CK.Chứng minh: B, I, N thẳng hàng.Bài 2: G là trọng tâm của tam giác ABC, G thuộc AG sao cho G là trung điểm của AG.a) So sánh các cạnh của tam giác BGG với các đường trung tuyến của tam giác ABC.b) So sánh các đường trung tuyến của tam giac BGG với các cạnh của tam giac ABC.Giải chi tiết nhá m.n. Tks m.n trước :)
Đọc tiếp
Bài 1:Cho tam giác ABC, trung tuyến AM, trọng tâm G. I, K thuộc tia đối AM sao cho MI=MG, IK=IG. N là tủng điểm của CK.
Chứng minh: B, I, N thẳng hàng.
Bài 2: G là trọng tâm của tam giác ABC, G' thuộc AG sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giac BGG' với các cạnh của tam giac ABC.
Giải chi tiết nhá m.n. Tks m.n trước :)
Cho tam giác ABC , đường trung tuyến AM . Trên tia đối của tia MA . Trên tia đối của tia MA lấy điểm D sao cho MD = 1/3 AM . Từ C vẽ một đường thẳng song song với BD cắt AM tại G . Chứng Minh Rằng G là trọng tâm của tam giác ABC
Cho tam giác ABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F
sao cho BE CF.
a) Chứng minh rằng 2 tam giác ABC và AEF có cùng trọng tâm (gọi trọng tâm chung đó là G)
b) AG cắt BC tại M. Gọi H là trung điểm AG, Nối EG cắt AF tại N. Lấy I là trung điểm EG.
Chứng minh IH // MN và IH MN
Đọc tiếp
Cho tam giác ABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F
sao cho BE = CF.
a) Chứng minh rằng 2 tam giác ABC và AEF có cùng trọng tâm (gọi trọng tâm chung đó là G)
b) AG cắt BC tại M. Gọi H là trung điểm AG, Nối EG cắt AF tại N. Lấy I là trung điểm EG.
Chứng minh IH // MN và IH = MN
Tam giác ABC có đường trung tuyến AM,trọng tâm G, trên tia đối của tia MA lấy 2 điểm I và K sao cho M là trung điểm của IG .Y là trung điểm KG.gọi N là trung điểm CK
A)Chứng minh I là trọng tâm của tam giác KBCb) Ba điểm BIN thẳng hàng
T
1. Cho tam giác ABC, trung tuyến AM. trên tia MA lấy điểm D sao cho MD = 1/3 AM. Gọi G là trọng tâm của tam giác ABC. So sánh các cạnh của tam giác BGD với các đường trung tuyến của tam giác ABC.
2. Cho tam giác ABC lấy T thuộc BC sao cho TB = 2/3 BC. Trên tia đối của tia CA lấy D sao cho DA = CA, đường thẳng DT cắt AB tại E. Chứng minh EA = EB.
Cho tam giác ABC(AB<AC) và AM là trung tuyến. Gọi G là trọng tâm của tam giác ABC, trên tia AM lấy điểm G' sao cho G là trung điểm của AC'
a) Chứng minh MG' = \(\frac{1}{2}\)AG
b) Chứng minh BG'=GC
c)Đường trung trực của cạnh BC lần lượt cắt các cạnh AC,Cg tại I và k. Chứng minh tam giác ICK = tam giác IBK
Hình như là điểm C đó cậu.Chắc mình gõ nhầm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC có đường trung tuyến am. trên tia đối của tia MA lấy điểm D. gọi G là trọng tâm của tam giác abc, cho biết MD= MG.
a. chứng mình BG song song CD
b.gọi I là trọng tâm của bd. H là giao điểm của AI và BM. chứng mình AM= 2 lần AI
a: Xét tứ giác BGCD có
M là trung điểm chung của BC và GD
=>BGCD là hình bình hành
=>BG//CD
Đúng 0
Bình luận (0)