một kệ sách chứa 7 quyển sách toán; 5 quyển sách ngữ văn; 3 quyển sách tiếng anh.Lấy ngẫu nhiên một quyển sách.Tĩnh xác suất để lấy được quyển sách không phải.

Những câu hỏi liên quan
Một kệ sách có 72 quyển sách Toán 6, 7, 8. Số sách Toán 6 bằng 2/3 tổng số sách. Số sách Toán 7 bằng 1/3 số sách toán 6. Tìm số sách toán 8?
sách 6 : 72x2/3=48(quyển) sách 7; 48x1/3=16(quyển) sách 8: 72-(48+16)=8(quyển) Đ/s:8 quyển sách toán 8
Đúng 0
Bình luận (0)
Một kệ sách có 72 quyển sách toán 6,7,8. Số sách toán 6 bằng 1/3 tổng số sách. Số sách toán 7 bằng 1/2 số sách toán 6. Tim số sách toán 8.
x là sách toán 6
y là sách toán 7
z là sách toán 8
Công thức :
x = 72 / 3 = 24
y = a / 2 = 24 / 2 = 12
z = 72 - ( 24 + 12 ) = 36
ĐS = z = 36
Đúng 0
Bình luận (0)
x là sách toán 6
y là sách toán 7
z là sách toán 8
Công thức :
x = 72 / 3 = 24
y = a / 2 = 24 / 2 = 12
z = 72 - ( 24 + 12 ) = 36
ĐS = z = 36
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trên một kệ sách có 6 quyển sách toán khác nhau, 7 quyển sách lý khác nhau và 8 quyển sách hóa khác nhau. Có bao nhiêu cách chọn 4 quyển sách khác nhau đủ cả ba loại sách toán, lý và hóa tặng cho 4 học sinh của lớp 11A1?
Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách
Đúng 0
Bình luận (0)
Có hai kệ sách A và B giống nhau và chứa các quyển sách giống nhau. Kệ A đã chứa được 3/4số sách. Kệ B đã chứa được 3/8 số sách. Nếu có 175 quyển sách cùng phân chia vào 2 kệ sách trên thì hai kệ sách đều đầy. Hỏi khi chứa đầy thì tổng số quyển sách ở hai kệ là bao nhiêu quyển?
may tu lam
bai nay ma ko biet
dung ! thi bam vao
Đúng 0
Bình luận (0)
có 8 quyển sách toán 7 quyển sách lý,5 quyển sách hóa được xếp lên cùng 1 kệ hỏi có bao nhiêu cách xếp thỏa mãn các sách toán phải xếp cạnh nhau
Coi 8 cuốn sách toán như 1 cuốn
=>Cần xếp 13 cuốn vào 13 vị trí khác nhau
=>Có 13! cách
Số cách xếp 8 cuốn sách toán là 8!(cách)
Số cách xếp là \(13!\cdot8!\)(cách)
Đúng 1
Bình luận (0)
Có hai kệ sách A và B giống nhau và chứa các quyển sách có kích thước giống nhau. Kệ A đã chứa được 3/4 số sách. Kệ B đã chứa được 3/8 số sách. Nếu có 175 quyển sách cùng kích thước được phân chia vào 2 kệ sách trên thì 2 kệ sách đều đầy. Hỏi khi chứa đầy thì tổng số sách trong 2 kệ là bao nhiêu quyển?
Một kệ sách có 48 quyển, trong đó có 12 quyển sách văn học và số còn lại là sách toán. Hỏi
a, Tỉ số sách văn học và sách toán là bao nhiêu?
b, Tỉ số sách toán và tổng số sách ở trên kệ là bao nhiêu?
Có 3 quyển sách Toán ; 4 quyển sách Văn và 5 quyển sách Anh. Hỏi có bao nhiêu cách sắp xếp 3 quyển sách Toán ; 3 quyển sách Văn và 3 quyển sách Anh
a) Vào 1 kệ dài ?
b) 1 kệ dài sao cho các quyển sách cùng loại nằm kề nhau?
Số cách chọn 3 quyển sách văn là \(C^3_4=4\).
Số cách chọn 3 quyển sách anh là \(C^3_5=10\).
a, Số cách sắp xếp vào 1 kệ dài là \(9!.4.10=14515200\) cách.
b, Coi số sách mỗi loại là một phần tử.
Số cách sắp xếp thỏa mãn yêu cầu bài toán là \(3!.4.10=240\) cách.
Đúng 2
Bình luận (0)
Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 7 quyển sách Tiếng Anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không ở cạnh nhau
A
.
19
12012
B
.
19
1012
C
.
19
1202
D
.
5...
Đọc tiếp
Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 7 quyển sách Tiếng Anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không ở cạnh nhau
A . 19 12012
B . 19 1012
C . 19 1202
D . 5 8008
Chọn A
|
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
| 1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
Gọi Ω là biến cố “xếp quyển sách lên kệ sách một cách tùy ý”
=> n( Ω ) = 14!
A là biến cố “xếp 14 cuốn sách lên kệ sách sao cho hai cuốn sách cùng môn không ở cạnh nhau”.
- Xếp quyển sách Tiếng Anh vào kệ có 7! cách.
- quyển sách Tiếng Anh tạo ra 8 chỗ trống (gồm 6 chỗ trống ở giữa và 2 chỗ trống trước sau).
Đánh số từ 1 đến 8, từ trái sang phải cho các chỗ trống. Khi đó ta xét các trường hợp:
TH1: Xếp sách Văn hoặc Toán vào vị trí từ 1 đến 7 có 7! cách.
TH2: Xếp sách Văn hoặc Toán vào vị trí từ 2 đến 8 có 7! cách.
TH3: Xếp cặp sách Văn – Toán chung vào ngăn, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại. Ta có:
+ Số cách chọn cặp sách Văn – Toán: 3.4 cách.
+ Vị trí 2 cuốn sách trong cặp sách: 2! cách.
+ Xếp các sách còn lại vào các ngăn 3,4,5,6,7 có 5! cách
Vậy ta có số cách xếp 1 cặp sách Văn – Toán chung vào ngăn 2, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại là 3.4.2!.5! cách.
Tương tự cho xếp cặp sách Văn – Toán lần lượt vào các ngăn 3,4,5,6,7
Số trường hợp thuận lợi của biến cố là ![]()
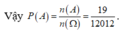
Đúng 0
Bình luận (0)
thư viện của một trường tiểu học đã xếp những quyển sách vào 15 kệ, mỗi kệ 126 quyển sách. Hỏi nếu mỗi kệ chứa 105 quyển thì cần bao nhiêu kệ để xếp hết số sách đó?
Thư viện của trường chứa số quyển sách là:
126 x 15=1890 (quyển)
Nếu mỗi kệ chứa 105 quyển sách thì cần số kệ để chứa số sách đó là:
1890 : 105=180(kệ)
Đáp số:18 kệ
Có tất cả số quyển sách là:
15*126=1890(quyển)
Nếu 1 kệ 105 quyển sách thì cần số kệ là:
1890:105=18(kệ)
Đáp số:18 kệ




























