Bài 8: Cho (O), có đường kính BC=8cm . Gọi H là trung điểm của OC ; vẽ dây AD vuông góc BC tại H. Cho AO cắt BD tại N
a) C/m tam giác ABD cân
b) C/m ABNH nội tiếp
c) Tính diện tích phần (O) nằm ngoài ABDC

Những câu hỏi liên quan
Cho tam giác ABC nội tiếp đường tròn (o) đường kính BC . Vẽ dây cung AD của (o) vuông góc với đường kính BC tại H . Gọi M là trung điểm cạnh OC và I là trung điểm cạnh AC . từ M vẽ đường thẳng vuông góc với OC , đường thẳng này cắt tia OI tại N . Trên tia ON lấy điểm S sao cho N là trung điểm cạnh OSa) c/m tam giác ABC vuông tại A và HA HDb) c/m : MN // SC và SC là tiếp tuyến của đường tròn (o)c) gọi K là trung điểm cạnh HC , vẽ đường tròng đường kính AH cắt cạnh AK tại F . C/m BH . HC AF . AK...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (o) đường kính BC . Vẽ dây cung AD của (o) vuông góc với đường kính BC tại H . Gọi M là trung điểm cạnh OC và I là trung điểm cạnh AC . từ M vẽ đường thẳng vuông góc với OC , đường thẳng này cắt tia OI tại N . Trên tia ON lấy điểm S sao cho N là trung điểm cạnh OS
a) c/m tam giác ABC vuông tại A và HA = HD
b) c/m : MN // SC và SC là tiếp tuyến của đường tròn (o)
c) gọi K là trung điểm cạnh HC , vẽ đường tròng đường kính AH cắt cạnh AK tại F . C/m BH . HC = AF . AK
d) Trên tia đối của tia BA lấy điểm E sao cho B là trung điểm cạnh AE . C/m ba điểm E,H,F thẳng hàng
Bài 2. Cho nửa đường tròn (O; R), có BC là đường kính. Trên đoạn OC lấy điểm H (H khác C và O). Qua H kẻ đường thẳng vuông góc với BC cắt nửa đường tròn tại A. Gọi E và F là hình chiếu của H trên AB, AC. Gọi D là giao điểm của AH với EF.1) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn;2) Chứng minh OA vuông góc với EF;3) Qua B kẻ đường thẳng vuông góc với CB, cắt đường thẳng CD tại K. Chứng minh AK // EF.
Đọc tiếp
Bài 2. Cho nửa đường tròn (O; R), có BC là đường kính. Trên đoạn OC lấy điểm H (H khác C và O). Qua H kẻ đường thẳng vuông góc với BC cắt nửa đường tròn tại A. Gọi E và F là hình chiếu của H trên AB, AC. Gọi D là giao điểm của AH với EF.1) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn;2) Chứng minh OA vuông góc với EF;3) Qua B kẻ đường thẳng vuông góc với CB, cắt đường thẳng CD tại K. Chứng minh AK // EF.
1: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
=>A,E,H,F cùng thuộc một đường tròn
2: Kẻ tiếp tuyến Ax tại A của (O)
Xét (O) có
\(\widehat{xAB}\) là góc tạo bởi tiếp tuyến Ax và dây cung AB
nên \(\widehat{xAB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BA}\)
Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn cung BA
Do đó: \(\widehat{ACB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BA}\)
=>\(\widehat{xAB}=\widehat{ACB}\left(1\right)\)
Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AEF}=\widehat{AHF}\)
mà \(\widehat{AHF}=\widehat{ACB}\left(=90^0-\widehat{HAC}\right)\)
nên \(\widehat{AEF}=\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{xAB}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//EF
Ta có: Ax//EF
OA\(\perp\)Ax
Do đó: OA\(\perp\)EF
Đúng 2
Bình luận (0)
1.Cho đường tròn (O,R8cm) đường kính AB và một điểm C thuộc đường tròn (O) sao cho ACR.a) Tính BC và số đo góc B,Cb)Đường cao CH trong tam giác ABC cắt đường tròn (O) tại D.Chứng minh H là trung điểm của CDc) Gọi I là trung điểm của BC,K là trung điểm của AC.Chứng minh CIOK là hình chữ nhật .Bài 2:Cho đường tròn (O,R) đường kính AB , M là trung điểm của OB. Vẽ da6y CD vuông góc với AB tại Ma) Chứng minh: OCBD là hình thoi. Tính diện tích OCBD theo Rb) Gọi E là điểm đối xứng của C qua O. Chứng mi...
Đọc tiếp
1.Cho đường tròn (O,R=8cm) đường kính AB và một điểm C thuộc đường tròn (O) sao cho AC=R.
a) Tính BC và số đo góc B,C
b)Đường cao CH trong tam giác ABC cắt đường tròn (O) tại D.Chứng minh H là trung điểm của CD
c) Gọi I là trung điểm của BC,K là trung điểm của AC.Chứng minh CIOK là hình chữ nhật .
Bài 2:Cho đường tròn (O,R) đường kính AB , M là trung điểm của OB. Vẽ da6y CD vuông góc với AB tại M
a) Chứng minh: OCBD là hình thoi. Tính diện tích OCBD theo R
b) Gọi E là điểm đối xứng của C qua O. Chứng minh CBDE là hình thang cân.
Bài 3:CHo tam giác ABC nội tiếp đường tròn (O). M là điểm bất kỳ trên cung BC không chứa A. Gọi D,E lần lượt là điểm đối xứng của M qua BC.
a) Chứng minh DE=2.AM.sin BAC
b) Xác định vị trí M để chu vi tam giác ADE lớn nhất
1.Cho đường tròn (O,R8cm) đường kính AB và một điểm C thuộc đường tròn (O) sao cho ACR.a) Tính BC và số đo góc B,Cb)Đường cao CH trong tam giác ABC cắt đường tròn (O) tại D.Chứng minh H là trung điểm của CDc) Gọi I là trung điểm của BC,K là trung điểm của AC.Chứng minh CIOK là hình chữ nhật .Bài 2:Cho đường tròn (O,R) đường kính AB , M là trung điểm của OB. Vẽ dây CD vuông góc với AB tại Ma) Chứng minh: OCBD là hình thoi. Tính diện tích OCBD theo Rb) Gọi E là điểm đối xứng của C qua O. Chứng min...
Đọc tiếp
1.Cho đường tròn (O,R=8cm) đường kính AB và một điểm C thuộc đường tròn (O) sao cho AC=R.
a) Tính BC và số đo góc B,C
b)Đường cao CH trong tam giác ABC cắt đường tròn (O) tại D.Chứng minh H là trung điểm của CD
c) Gọi I là trung điểm của BC,K là trung điểm của AC.Chứng minh CIOK là hình chữ nhật .
Bài 2:Cho đường tròn (O,R) đường kính AB , M là trung điểm của OB. Vẽ dây CD vuông góc với AB tại M
a) Chứng minh: OCBD là hình thoi. Tính diện tích OCBD theo R
b) Gọi E là điểm đối xứng của C qua O. Chứng minh CBDE là hình thang cân.
Bài 3:CHo tam giác ABC nội tiếp đường tròn (O). M là điểm bất kỳ trên cung BC không chứa A. Gọi D,E lần lượt là điểm đối xứng của M qua BC.
a) Chứng minh DE=2.AM.sin BAC
b) Xác định vị trí M để chu vi tam giác ADE lớn nhất
Bài 4: Cho đường tròn tâm O đường kính AC. Trên đoạn thẳng OC lấy điểm B và vẽ đường tròn O’ có đường kính BC. Gọi M là trung điểm của AB, qua M kẻ dây cung vuông góc với AB cắt đường tròn O tại D và E. Nối CD cắt đường tròn O’ tại Ia/ Chứng minh DAEB là hình gì?b/ Chứng minh MI MD và MI là tiếp tuyến của đường tròn O’c/ Gọi H là hình chiếu của I trên BC. Chứng minh CH.MB BH.MCMn giúp em với ạ, cảm ơn mn nhìu :
Đọc tiếp
Bài 4: Cho đường tròn tâm O đường kính AC. Trên đoạn thẳng OC lấy điểm B và vẽ đường tròn O’ có đường kính BC. Gọi M là trung điểm của AB, qua M kẻ dây cung vuông góc với AB cắt đường tròn O tại D và E. Nối CD cắt đường tròn O’ tại I
a/ Chứng minh DAEB là hình gì?
b/ Chứng minh MI = MD và MI là tiếp tuyến của đường tròn O’
c/ Gọi H là hình chiếu của I trên BC. Chứng minh CH.MB= BH.MC
Mn giúp em với ạ, cảm ơn mn nhìu :>
Tam giác ABC nội tiếp đường tròn (O;R) đường kính BC. Vẽ dây cung AD của (O) vuông góc với đường kính BC tại H. gọi M là trung điểm của OC và I là trung điểm của AC. Từ M vẽ đường thẳng vuông góc với AC đường thẳng này cắt tia OI tại N. Trên tia ON lấy điểm S sao cho N là trung điểm của OS a) Cho R 5cm, AB 6 cm. Tính AH b) chứng minh 4 điểm A, H, O, I cùng thuộc một đường tròn c) chứng minh SC là tiếp tuyến của (O) d) gọi K là trung điểm HC, vẽ đường tròn đường kính AH cắt cạnh AK tại F. chứng...
Đọc tiếp
Tam giác ABC nội tiếp đường tròn (O;R) đường kính BC. Vẽ dây cung AD của (O) vuông góc với đường kính BC tại H. gọi M là trung điểm của OC và I là trung điểm của AC. Từ M vẽ đường thẳng vuông góc với AC đường thẳng này cắt tia OI tại N. Trên tia ON lấy điểm S sao cho N là trung điểm của OS
a) Cho R= 5cm, AB = 6 cm. Tính AH
b) chứng minh 4 điểm A, H, O, I cùng thuộc một đường tròn
c) chứng minh SC là tiếp tuyến của (O)
d) gọi K là trung điểm HC, vẽ đường tròn đường kính AH cắt cạnh AK tại F. chứng minh HB x AC = AF x AK
Cho tam giác ABC nội tiếp đường tròn (o) đường kính BC . Vẽ dây cung AD của (o) vuông góc với đường kính BC tại H . Gọi M là trung điểm cạnh OC và I là trung điểm cạnh AC . từ M vẽ đường thẳng vuông góc với OC , đường thẳng này cắt tia OI tại N . Trên tia ON lấy điểm S sao cho N là trung điểm cạnh OS a) c/m tam giác ABC vuông tại A và HA HDb) c/m : MN // SC và SC là tiếp tuyến của đường tròn (o)c) gọi K là trung điểm cạnh HC , vẽ đường tròng đường kính AH cắt cạnh AK tại F . C/m BH . HC AF . A...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (o) đường kính BC . Vẽ dây cung AD của (o) vuông góc với đường kính BC tại H . Gọi M là trung điểm cạnh OC và I là trung điểm cạnh AC . từ M vẽ đường thẳng vuông góc với OC , đường thẳng này cắt tia OI tại N . Trên tia ON lấy điểm S sao cho N là trung điểm cạnh OS
a) c/m tam giác ABC vuông tại A và HA = HD
b) c/m : MN // SC và SC là tiếp tuyến của đường tròn (o)
c) gọi K là trung điểm cạnh HC , vẽ đường tròng đường kính AH cắt cạnh AK tại F . C/m BH . HC = AF . AK
d) Trên tia đối của tia BA lấy điểm E sao cho B là trung điểm cạnh AE . C/m ba điểm E,H,F thẳng hàng
Bài 1 trên nửa đương tròn tâm O , đường kính AB = 8cm , dựng dây AB = 4cm và tiếp tuyến Ax . Tia BC cắt Ax tại D . Gọi K là trung điểm của AD.
a) tính BC,CD
b) chứng minh KC là tiếp tuyến của đường tròn tâm O
Bài 5:Cho tam giác ABC vuông tại A, có AB 8 cm; AC 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.a)Tính độ dài đoạn BC và AMb)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.c) Chứng minh tứ giác OACE nội tiếp Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (MBC, NAC). Hai đường cao AM và BN cắt nhau tại H.a)Chứng minh rằng tứ giác CMHN nội tiếp một đường trònb)Chứng minh rằng AM.CH AC.MN
Đọc tiếp
Bài 5:Cho tam giác ABC vuông tại A, có AB = 8 cm; AC = 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.
a)Tính độ dài đoạn BC và AM
b)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.
c) Chứng minh tứ giác OACE nội tiếp
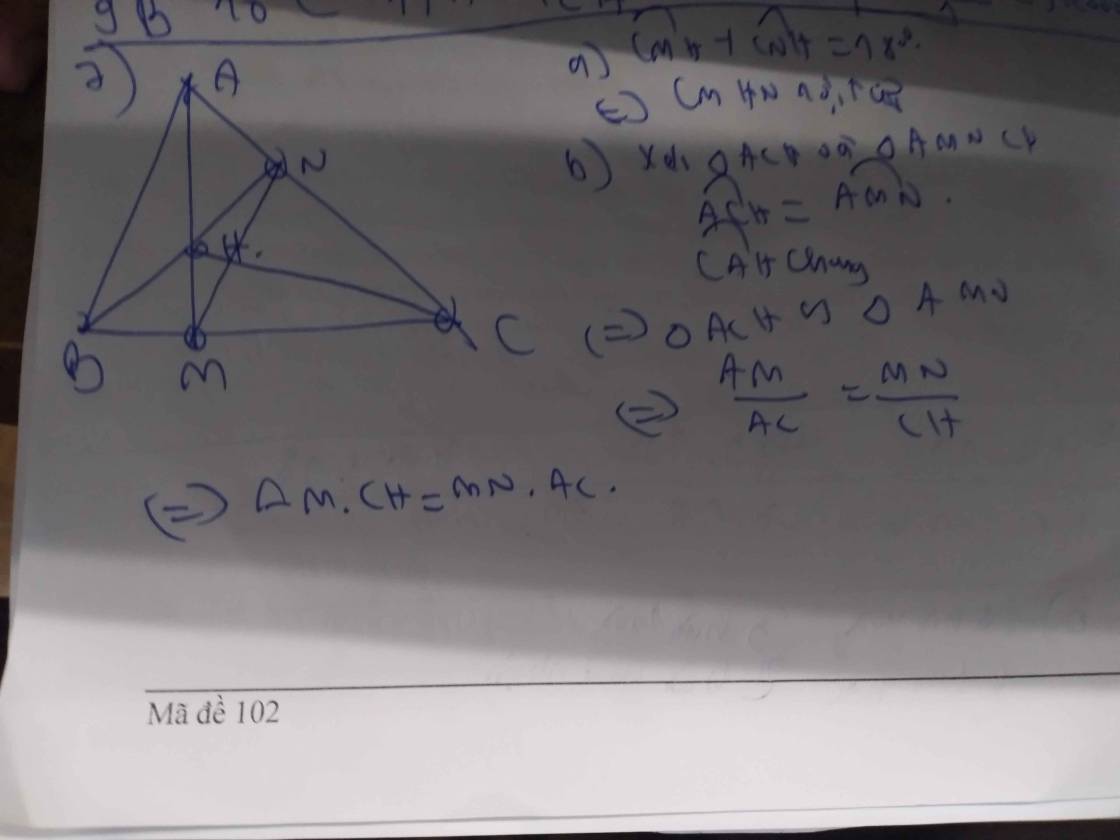
Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (M=BC, N=AC). Hai đường cao AM và BN cắt nhau tại H.
a)Chứng minh rằng tứ giác CMHN nội tiếp một đường tròn
b)Chứng minh rằng AM.CH = AC.MN
Bài 1: Cho tam giác ABC cân tại A, nội tiếp đường tròn(O). Đường cao AH cắt đường tròn ở D.a) Vì sao AD là đường kính của đường tròn(O)b) Tính góc ∠ACDc) Cho BC 24cm; AC 20cm. Tính đường cao AH và bán kính đường tròn(O)Bài 2: Cho tam giác ABC nội tiếp đường tròn (O;R). Gọi M là trung điểm BC. Giả sử O nằm trong tam giác AMC hoặc O nằm giữa A và M. Gọi I là trung điểm AC. CMR:a) Chu vi tam giác IMC lớn hơn 2Rb) Chu vi tam giác ABC lớn hơn 4RBài 3: Cho tam giác ABC có D, E, F theo thứ tự là trun...
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, nội tiếp đường tròn(O). Đường cao AH cắt đường tròn ở D.
a) Vì sao AD là đường kính của đường tròn(O)
b) Tính góc ∠ACD
c) Cho BC = 24cm; AC = 20cm. Tính đường cao AH và bán kính đường tròn(O)
Bài 2: Cho tam giác ABC nội tiếp đường tròn (O;R). Gọi M là trung điểm BC. Giả sử O nằm trong tam giác AMC hoặc O nằm giữa A và M. Gọi I là trung điểm AC. CMR:
a) Chu vi tam giác IMC lớn hơn 2R
b) Chu vi tam giác ABC lớn hơn 4R
Bài 3: Cho tam giác ABC có D, E, F theo thứ tự là trung điểm BC, CA, AB. G, H, I theo thứ tự là chân đường cao từ đỉnh A, B, C. Trực tâm tam giác ABC là S. J, K, L theo thứ tự là trung điểm của SA, SB, SC. Chứng minh rằng: 9 điểm D, E, F, G, H, I, J, K, L cùng thuộc đường tròn. ( Gợi ý: đường tròn đường kính JD)
Bài 4: Cho tam giác ABC nội tiếp(O), H là trực tâm tam giác ABC. Gọi D, E, F thứ tự là trung điểm của BC, CA, AB. Đường tròn tâm D bán kính DH cắt BC tại A1, A2, đường tròn tâm E bán kính EH cắt CA tại B1, B2, đường tròn tâm F bán kính FH cắt AB tại C1, C2.
a) : Chứng minh 3 đường thẳng DD' , EE' , FF' đồng quy ( DD' song song với OA, EE' song songvới OB, FF' song song với OC ).
b) Chứng minh 6 điểm A1, A2, B1, B2, C1, C2 nằm trên một đường tròn.
Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5