a, Cho định lí:Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông
-hãy cho biết giả thiết của định lí
-hãy cho bik kết luận của định lí
- chứng minh định lí trên
Cảm ơn các bn nhìu lắm!
cho định lí : Góc tạo bởi hai tia phân giác của 2 góc kề bù là 1 góc vuông
- Hãy cho biết giả thiết của định lí
- Hãy cho biết kết luận của định lí
- Hãy chứng minh định lí trên
b, cho định lí :nếu 1 đường thẳng cắ 2 đường thẳng phân biệt và trong số các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau
- Hãy cho biết giả thiết của định lí đó
- Hãy cho biết kết luận của định lí đó
- Hãy chứng minh định lí đó
Nhanh là 1 Like nha !!!!!!!!!!!!!!!!!!
khó thì 10 like cũng ko được nữa là 1 like
a)
giả thiết vs kết luận bạn tự ghi nha, có đó dễ.
c/m:
gọi x và y là số đo góc tạo bởi 2 tia phân giác của 2 góc kề bù.
ta có: 2x + 2y= 180 độ
suy ra x+y = 180/2=90 độ
Bài 1 :
Giả thiết : Góc tạo bởi hai tia phân giác của 2 góc kề bù
Kết luận : là 1 góc vuông
Chứng minh :
gọi x và y là số đo góc tạo bởi 2 tia phân giác của 2 góc kề bù.
ta có: 2x + 2y= 180 độ
suy ra x+y = \(\dfrac{180^o}{90^o}\)=90 độ
Bài 2:
Giả thiết: Nếu một đường thẳng cắt 2 đường thẳng phân biệt trogn số các góc tạo thành có một cặp góc so le trong bằng nhau
Kết luận: thì các cặp góc đồng vị bằng nhau.
Hướng dẫn nha:
Bạn vẽ hai đường thẳng phân biệt song song vs nhau
Vẽ một đường thẳng bất kì đi qua 2 đưuòng thẳng song song đó.
Khi đó sẽ tạo thành hai cặp góc so le trong và đồng vị bằng nhau.
Cho định lí : Góc tạo bởi hai tia phân giác của hai góc kế bù là một góc vuông .
-Hãy cho bík giả thuyết của định lí .
-Hãy cho bík kết luận của định lí .
-Hãy chứng minh định lí trên
- Giả thuyết: cho góc tạo bởi 2 tia phân giác của 2 góc kề bù
- Kết luận: đó là 1 góc vuông
- Chứng minh:
Ta có hình vẽ:
Do Om là tia phân giác của góc zOy => góc \(zOm=mOy=\frac{1}{2}.zOy\)
Do On là tia phân giác của góc xOz => góc \(xOn=nOz=\frac{1}{2}.xOz\)
Ta có:
zOy + xOz = 180o (kề bù)
=> \(\frac{1}{2}.zOy+\frac{1}{2}.xOz=\frac{1}{2}.180^o\)
=> zOm + zOn = 90o
Lại có: zOn + zOm = mOn => mOn = 90o là góc vuông (đpcm)
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy viết giả thiết và kết luận của định lí
Cho định lí : "Hai tia phân giác của hai góc kề bù tạo thành một góc vuông" (hình vẽ). Gỉa thiết, kết luận của định lí là:
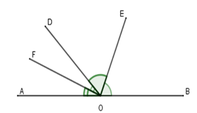
A. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF
B. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOF; OF là phân giác góc AOD.
Kết luận: OE⊥OA
C. Giả thiết: Cho góc bẹt AOB và tia OD.OE là phân giác góc BOD; OF là phân giác góc AOE.
Kết luận: OE⊥OF
D. Giả thiết: Cho góc bẹt AOBAOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AODAOD.
Kết luận: OB⊥OF
Đáp án C
Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF
2 : Phát biểu tính chất : " Hai tia phân giác của 2 góc kề bù tạo thành góc vuông " thành định lí dạng : Nếu.... thì
rồi vẽ hình và ghi Giả thiết , kết luận của định lí
Chứng minh định lí và phát biểu
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
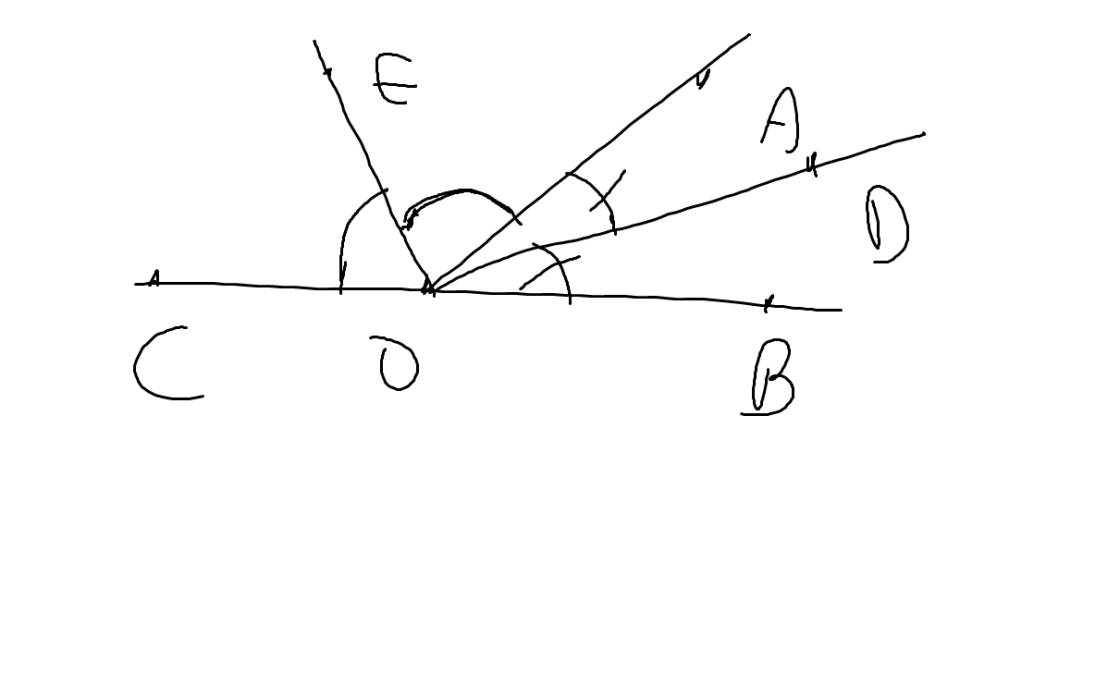
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
cho định lí " tia phân giác của hai góc kề bù thì vuông góc với nhau"
a) vẽ minh họa định lí trên
b) viết giả thiết, két luận của định lí trên
mong các bạn giúp mình với
a: 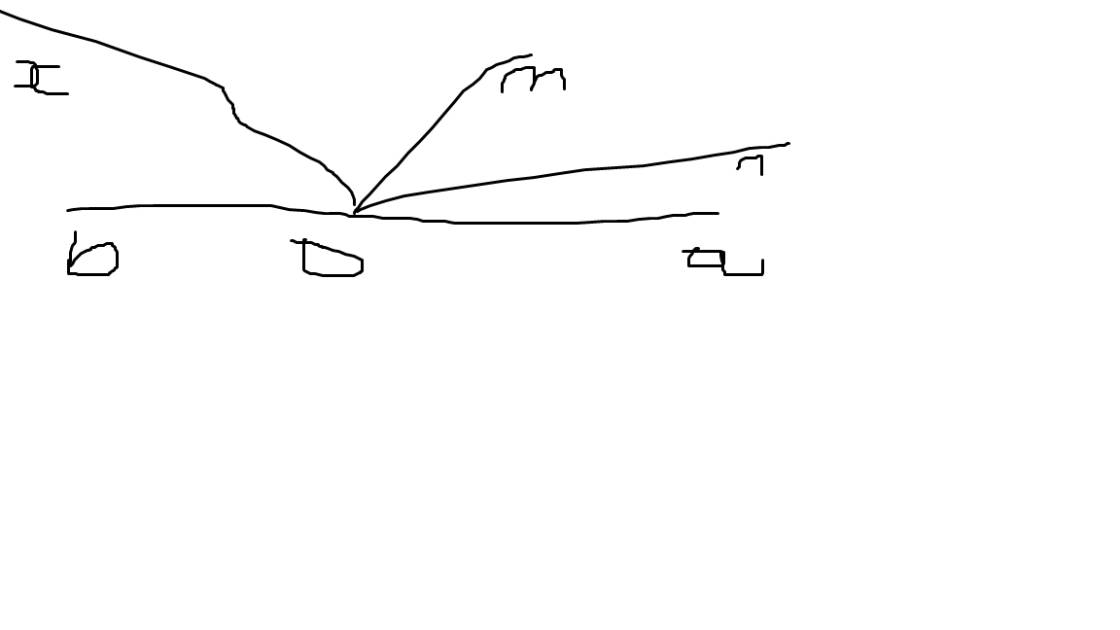
b:
| GT | góc aOm và góc bOm là hai góc kề bù On,Ox lần lượt là phân giác của góc aOm và góc bOm |
| KL | góc xOn=90 độ |
Cho định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông
-Chứng minh định lí trên
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
* Vẽ hình: Vẽ hình hơi xấu chút! ![]()
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
Chứng minh :
\(\widehat{mOz=\frac{1}{2}}\widehat{xOz}\) \(\left(1\right)\) ( vì Om là hai tia phân giác của \(\widehat{xOz}\) )
\(\widehat{zOn}=\frac{1}{2}\widehat{zOy}\) \(\left(2\right)\) ( vì On là hai tia phân giác của \(\widehat{zOy}\) )
Từ \(\left(1\right)\) và \(\left(2\right)\) , ta có :
\(\widehat{mOz}+\widehat{zOn}=\frac{1}{2}.\left(\widehat{xOz}+\widehat{zOy}\right)\) \(\left(3\right)\)
Vì tia \(Oz\) nằm giữa hai tia \(Om,On\) và vì \(\widehat{xOz}\) và \(\widehat{zOy}\) kề bù \(\left(gt\right)\)
Nên từ \(\left(3\right)\) \(\Rightarrow\widehat{mOn}=\frac{1}{2}.180^0\)
Hay \(\widehat{mOn}=90^0\)
b) Cho Định lí : Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau .
- Hãy cho biết giả thiết của định lí đó .
- Hãy cho biết kết luận của định lí đó .
- Hãy chứng minh định lí đó .
- Gỉa thiết: Một đường thẳng cắt 2 đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau
- Kết luận: Các góc đồng vị bằng nhau
giả thiết luôn luôn đứng trước chữ thì còn kết luận sẽ đứng sau chữ thì ok bạn vẽ hình ra tìm đâu là cặp góc SlT rồi chứng minh nó bằng nhau thì ta suy ra đc các góc đồng vị bằng nhau trong sách hình như có hướng dẫn mà
Với hai góc kề bù, ta có định lí sau :
Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
a) Hãy vẽ hai góc xOy và yOx' kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot' của góc yOx' và gọi số đo của góc xOy là \(m^0\)
b) Hãy viết giả thiết và kết luận của định lí
c) Hãy điền vào chỗ trống (.....) và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên
1) \(\widehat{tOy}=\dfrac{1}{2}m^0\) vì .............
2) \(\widehat{t'Oy}=\dfrac{1}{2}\left(180^0-m^0\right)\) vì ..........
3) \(\widehat{tOt'}=90^0\) vì .............
4) \(\widehat{x'Oy}=180^0-m^0\) vì ..........