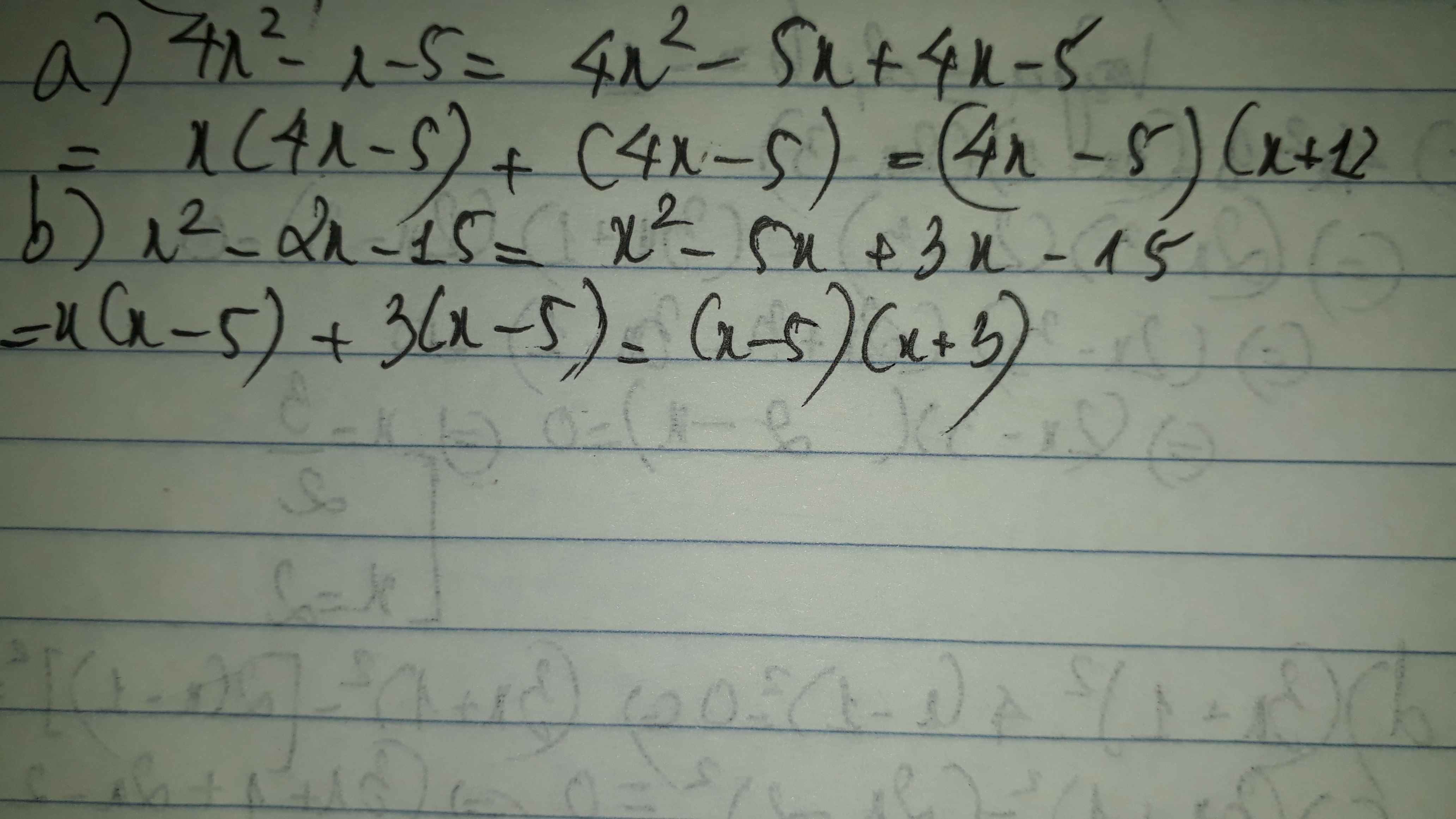phân tích đa thức bằng phương pháp tách các hạng tử:   x2+x-42

x²+x-42

=x²-6x+7x-42

=x.(x-6)+7.(x-6)

=(x-6)(x+7)

\(x^2+x-42=x^2+7x-6x-42=x\left(x+7\right)-6\left(x+7\right)=\left(x-6\right)\left(x+7\right)\)

phương pháp này mình gọi là phương pháp nhẩm nghiệm:

- Nếu tổng tất cả các hệ số bằng o thì đa thức có 1 nghiệm là x=1 hay chứa thừa số là x-1

- Nếu tổng tất cả các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ thì đa thức có một nghiệm là x=-1 hay chứa thừa số là x+1

a) 8x² - 2x - 1

=8x²+2x-4x-1

=2x.(4x+1)-(4x+1)

=(4x+1)(2x-1)

b) x² - y² + 10x - 6y + 16

=x²+10x+25-y²-6y-9

=(x+5)²-(y+3)²

=(x+5-y-3)(x+5+y+3)

=(x-y+2)(x+y+8)

\(6x^2+20x+6=6x^2+18x+2x+6\)

\(=6x\left(x+3\right)+2\left(x+3\right)\)

\(=\left(x+3\right)\left(6x+2\right)\)

\(=2\left(x+3\right)\left(3x+1\right)\)

x³-3x²-4=

\(x^4+x^2+1=x^4+1+2x^2-x^2=\left(x^2+1\right)^2-x^2=\left(x^2+1-x\right)\left(x^2+1+x\right)\)

a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)

b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)

\(x^3+3x^2-4\)

\(=\left(x^3+4x^2\right)-\left(x^2+4\right)\)

\(=\left(x^2+4\right)\left(x-1\right)\)

Mình nhìn nhầm đề

\(x^3+3x^2-4\)

\(=\left(x^3+2x^2\right)+\left(x^2-4\right)\)

\(=x^2\left(x+2\right)+\left(x-2\right)\left(x+2\right)\)

\(=\left(x+2\right)\left(x^2+x-2\right)\)

\(=\left(x+2\right)\left[\left(x^2+x\right)-\left(2x+2\right)\right]\)

\(=\left(x+2\right)\left(x+2\right)\left(x-1\right)\)

\(=\left(x+2\right)^2\left(x-1\right)\)