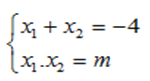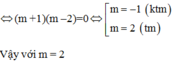c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4

Theo Vi-et ta có: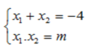 

Ta có: x 1 2 + x 2 2  = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10

⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)

Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn:  x 1 2 + x 2 2  = 10

\(\Delta=\left(m+1\right)^2-4.1.2=\left(m+1\right)^2-8\)

Để PT có 2 nghiệm thì:

\(\Delta\ge0\Leftrightarrow\left(m+1\right)^2-8\ge0\\ \Leftrightarrow\left(m+1\right)^2\ge8\)

Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=-\left(m+1\right)\\x_1x_2=2\end{matrix}\right.\)

\(x_1^2+x_2^2=x_1^2+2x_1x_2+x_2^2-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2\)

\(=\left(m+1\right)^2-2.2=\left(m+1\right)^2-4\)

Mà \(\left(m+1\right)^2\ge8\) nên \(\left(m+1\right)^2-4\ge4\)

\(\Rightarrow min_{x_1^2+x_2^2}=4\) (dấu bằng xảy ra)

\(\Leftrightarrow\left(m+1\right)^2=8\)

\(\Leftrightarrow m^2+2m+1=8\\\Leftrightarrow m^2+2m-7=0 \)

\(\Leftrightarrow m=-1\pm2\sqrt{2}\)

Bổ sung thêm điều kiện đề với \(m\ne1\) nữa nhé: )

Nhẩm nghiệm: \(a-b+c=0\) \(\left(m-1-m-1+2=0\right)\)

\(\Rightarrow\) PT có 2 nghiệm \(x_1=-1;x_2=\dfrac{2}{m-1}\)

Nếu \(x_1^2-x_2^2=3\):

\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=3\)

=> Không có giá trị m thỏa mãn.

Nếu \(x_1^2-x_2^2=-3\):

\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=-3\\ \Rightarrow m=2\left(TM\right)\)

a) Khi m = -5 ta được phương trình x2 + 4x - 5 = 0

Ta có a + b + c = 1 + 4 + (-5) = 0 nên phương trình có hai nghiệm phân biệt là x1 = 1; x2= c/a = (-5)/1 = -5

Tập nghiệm của phương trình S = {1; -5}

b) Δ' = 22 - m = 4 - m

Phương trình có nghiệm kép ⇔ Δ'= 0 ⇔ 4 - m = 0 ⇔ m = 4

c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4

Theo Vi-et ta có: 

Ta có: x12 + x22 = 10 ⇔ (x1 + x2)2 - 2x1x2 = 10

⇔ (-4)2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)

Đáp án A

\(\Delta'=m^2+2m+6=\left(m+1\right)^2+5>0\) ;\(\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-2m-6\end{matrix}\right.\)

Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)

\(P=\left(-2m\right)^2-2\left(-2m-6\right)=4m^2+4m+12\)

\(P=\left(2m+1\right)^2+11\ge11\)

\(P_{min}=11\) khi \(m=-\dfrac{1}{2}\)

a. Em tự giải

b.

\(\Delta'=\left(m-1\right)^2-\left(m^2-6\right)=-2m+7\)

Pt đã cho có 2 nghiệm khi: \(-2m+7\ge0\Rightarrow m\le\dfrac{7}{2}\)

Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-6\end{matrix}\right.\)

\(x_1^2+x_2^2=16\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)

\(\Leftrightarrow4\left(m-1\right)^2-2\left(m^2-6\right)=16\)

\(\Leftrightarrow2m^2-8m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=4>\dfrac{7}{2}\left(loại\right)\end{matrix}\right.\)

Vậy \(m=0\)

Lời giải:

Để PT có 2 nghiệm $x_1,x_2$ thì:

$\Delta'=(m+1)^2-(m^2-1)>0\Leftrightarrow 2m+2>0\Leftrightarrow m>-1$

Áp dụng định lý Viet:

$x_1+x_2=2(m+1)$ và $x_1x_2=m^2-1$

Khi đó, để $x_1^2+x_2^2=x_1x_2+8$

$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=x_1x_2+8$

$\Leftrightarrow (x_1+x_2)^2=3x_1x_2+8$

$\Leftrightarrow 4(m+1)^2=3(m^2-1)+8$

$\Leftrightarrow m^2+8m-1=0$

$\Leftrightarrow m=-4\pm \sqrt{17}$. Vì $m>-1$ nên $m=-4+\sqrt{17}$