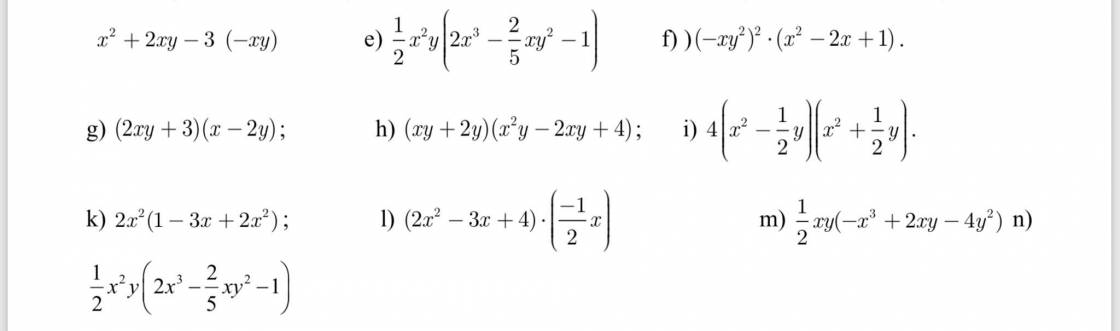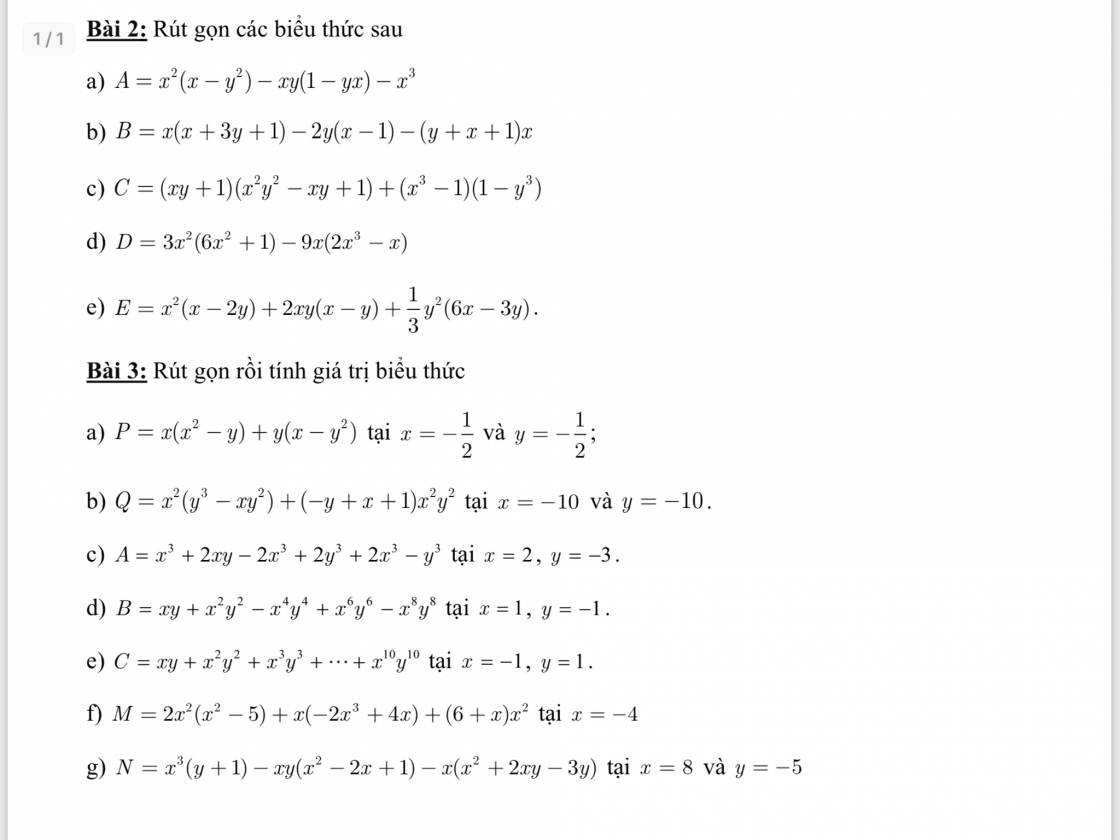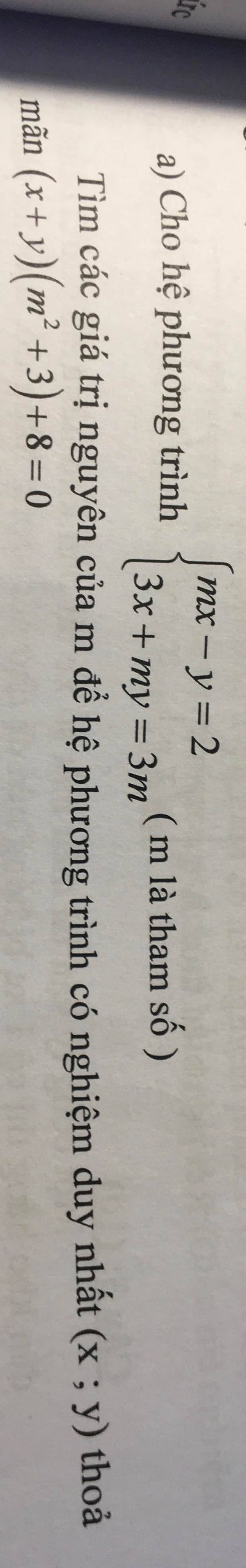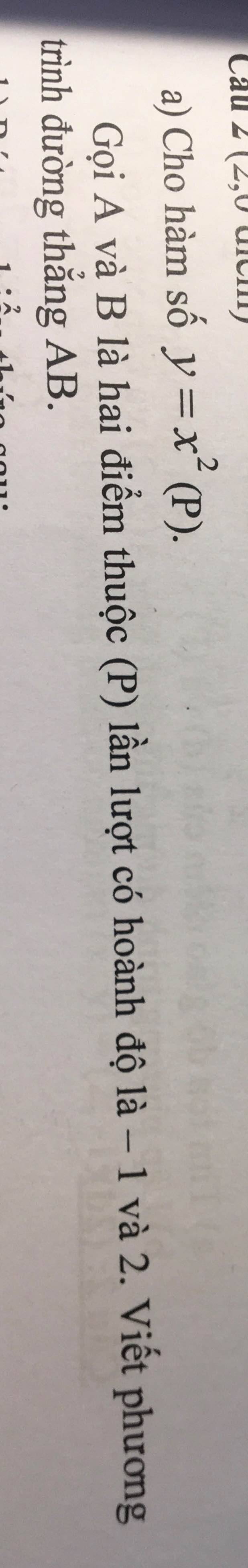\(a,\frac{13}{x-1}+\frac{5}{2x-2}-\frac{6}{3x-3}=3\)

\(\Leftrightarrow\frac{13}{x-1}+\frac{5}{2\left(x-1\right)}-\frac{6}{3\left(x-1\right)}\)

\(\Leftrightarrow\frac{13.2+5-4}{2\left(x-1\right)}=3\)

\(\Leftrightarrow6\left(x-1\right)=27\)

\(\Leftrightarrow x-1=\frac{9}{2}\Leftrightarrow x=\frac{11}{2}\)

\(b,\frac{2x}{3}-\frac{3}{4}>0\)

\(\Leftrightarrow\frac{8x-9}{12}>0\)

\(\Leftrightarrow8x-9>0\Rightarrow x>\frac{9}{8}\)

Câu 4: 

Thay x=2 và y=-1 vào hệ, ta được:

\(\left\{{}\begin{matrix}2a-b=4\\2b+2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\a=1\end{matrix}\right.\)

Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)

=>\(m^2\ne-3\)(luôn đúng)

Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)

\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)

=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)

=>\(3m^2+5m-6+8=0\)

=>\(3m^2+5m+2=0\)

=>(m+1)(3m+2)=0

=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)

Bài 2:

Thay x=-1 vào (P), ta được:

\(y=\left(-1\right)^2=1\)

Thay x=2 vào (P), ta được:

\(y=2^2=4\)

vậy: A(-1;1); B(2;4)

Gọi (d): y=ax+b(a\(\ne\)0) là phương trình đường thẳng AB

Thay x=-1 và y=1 vào (d), ta được:

\(a\cdot\left(-1\right)+b=1\)

=>-a+b=1(1)

Thay x=2 và y=4 vào (d), ta được:

\(2\cdot a+b=4\)

=>2a+b=4(2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-3a=-3\\-a+b=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=1\\b=a+1=1+1=2\end{matrix}\right.\)

Vậy: phương trình AB là y=x+2

Trong mp đáy, qua B kẻ đường thẳng song song AC, lần lượt cắt DA và DC kéo dài tại E và F

\(\Rightarrow AC||\left(SEF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SEF\right)\right)=d\left(A;\left(SEF\right)\right)\)

Gọi I là giao điểm AC và BD

Theo định lý Talet: \(\dfrac{ID}{IB}=\dfrac{DC}{AB}=3\Rightarrow\dfrac{ID}{BD}=\dfrac{3}{4}\)

Cũng theo Talet: \(\dfrac{DA}{DE}=\dfrac{DI}{DB}=\dfrac{3}{4}\Rightarrow AD=\dfrac{3}{4}DE\Rightarrow AE=\dfrac{1}{4}DE\)

\(\Rightarrow d\left(A;\left(SEF\right)\right)=\dfrac{1}{4}d\left(D;\left(SEF\right)\right)\)

Trong tam giác vuông EDF, kẻ \(DH\perp EF\) , trong tam giác vuông SDH, kẻ \(DK\perp SH\)

\(\Rightarrow DK\perp\left(SEF\right)\Rightarrow DK=d\left(D;\left(SEF\right)\right)\)

\(DE=\dfrac{4}{3}AD=\dfrac{4a}{3}\); \(DF=\dfrac{4}{3}DC=4a\)

\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{5}{8a^2}\)

\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{DH^2}=\dfrac{1}{48a^2}+\dfrac{5}{8a^2}\Rightarrow DK=\dfrac{4a\sqrt{93}}{31}\)

\(\Rightarrow d\left(AC;SB\right)=\dfrac{1}{4}DK=\dfrac{a\sqrt{93}}{31}\)