cho lăng trụ đứng ABC.A'B'C' có diên tích đáy bằng 2a2 góc giửa (A'BC) và (ABC) bằng 60o. khoảng cahcs từ B' đến (A'BC) bằng a. tính thể tích của khối trụ đã cho
Những câu hỏi liên quan
Cho lăng trụ đứng ABC.ABC có cạnh BC2a, góc giữa hai mặt phẳng (ABC) và (ABC) bằng
60
°
. Biết diện tích của tam giác
∆
A
B
C
bằng
2
a
2
. Tính thể tích V của khối lăng trụ ABC.ABC. A.
V
a
3
3
B.
V...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có cạnh BC=2a, góc giữa hai mặt phẳng (ABC) và (A'BC) bằng 60 ° . Biết diện tích của tam giác ∆ A ' B C bằng 2 a 2 . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = a 3 3
B. V = 2 a 3 3
C. V = a 3 3 3 .
D. V = 3 a 3
Cho lằng trụ đứng ABC.ABC có cạnh BC2a, góc giữa hai mặt phẳng (ABC) và (ABC) bằng
60
0
. Biết diện tích của tam giác ABC bằng
2
a
2
. Tính thể tích V của khối lăng trụ ABCABC. A.
V
3
a
3
B.
V
a
3
3
C.
V
2...
Đọc tiếp
Cho lằng trụ đứng ABC.A'B'C' có cạnh BC=2a, góc giữa hai mặt phẳng (ABC) và (A'BC) bằng 60 0 . Biết diện tích của tam giác A'BC bằng 2 a 2 . Tính thể tích V của khối lăng trụ ABCA'B'C.
A. V = 3 a 3
B. V = a 3 3
C. V = 2 a 3 3
D. V = a 3 3 3
Cho khối lăng trụ đứng ABC.ABC có đáy là tam giác đều. Mặt phẳng (ABC) tạo với đáy góc và tam giác ABC có diện tích bằng
8
a
2
. Tính thể tích V của khối lăng trụ đã cho.
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều. Mặt phẳng (A'BC) tạo với đáy góc và tam giác A'BC có diện tích bằng 8 a 2 . Tính thể tích V của khối lăng trụ đã cho.
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại B, BCa, mặt phẳng (ABC) tạo với đáy một góc
30
o
và tam giác ABC có diện tích bằng
a
2
3
. Tính thể tích khối lăng trụ ABC.ABC. A.
3
a
3...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, BC=a, mặt phẳng (A'BC) tạo với đáy một góc 30 o và tam giác A'BC có diện tích bằng a 2 3 . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. 3 a 3 3 2
B. 3 a 3 3 8
C. a 3 3 8
D. 3 a 3 3 4
Cho khối lăng trụ đứng ABC.ABC có đáy là tam giác đều. Mặt phẳng (ABC) tạo với đáy góc
30
0
và tam giác ABC có diện tích bằng 8. Tính thể tích V của khối lăng trụ đã cho.
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều. Mặt phẳng (A'BC) tạo với đáy góc 30 0 và tam giác A'BC có diện tích bằng 8. Tính thể tích V của khối lăng trụ đã cho.
Cho hình lăng trụ tam giác đều ABC.ABC có cạnh đáy bằng 2a, khoảng cách từ A đến mặt phẳng (ABC) bằng
v
Thể tích của khối lăng trụ đã cho bằng A.
3
a
3
B.
a
3
C.
4
3
a
3
3
.
D.
3...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2a, khoảng cách từ A đến mặt phẳng (A'BC) bằng v Thể tích của khối lăng trụ đã cho bằng
A. 3 a 3
B. a 3
C. 4 3 a 3 3 .
D. 3 a 3 4 .
Cho hình lăng trụ đứng ABC.ABC, biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (ABC) bằng
a
6
. Thể tích khối lăng trụ ABC.ABC là: A.
3
a
3
12
16
B.
3
a
3...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C', biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng a 6 . Thể tích khối lăng trụ ABC.A'B'C' là:
A. 3 a 3 12 16
B. 3 a 3 12 8
C. 3 a 3 2 28
D. 3 a 3 2 4
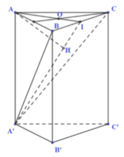
Phương pháp:
Thể tích khối lăng trụ: V = Sh
Cách giải:
Gọi I là trung điểm của BC, kẻ AH ⊥ A'I
∆
ABC đều cạnh a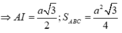 
Ta có:
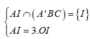
Ta có: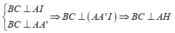 
Mà 
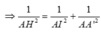
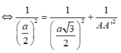
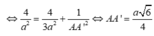
Chọn: A
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại B, BC a, mặt phẳng (ABC) tạo với đáy một góc 30
°
và tam giác có diện tích bằng
a
2
3
. Tính thể tích khối lăng trụ ABC.ABC. A.
3
a
3
3
2
B.
3
a...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, BC = a, mặt phẳng (A'BC) tạo với đáy một góc 30 ° và tam giác có diện tích bằng a 2 3 . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. 3 a 3 3 2
B. 3 a 3 3 8
C. a 3 3 8
D. 3 a 3 3 4
Phương pháp:
Xác định góc 30 ° (góc tạo bởi hai mặt phẳng là góc giữa hai đường thẳng cùng vuông góc với giao tuyến).
Tính diện tích tam giác đáy và chiều cao lăng trụ rồi tính thể tích theo công thức V = B.h
Cách giải:
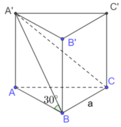
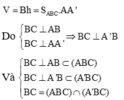
Ta có:
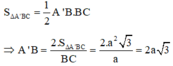
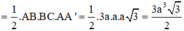
Chọn A.
Đúng 0
Bình luận (0)
Cho hình lăng trụ đều ABC.ABC có góc giữa đường thẳng AB với mặt phẳng (ABC) bằng
60
0
và khoảng cách từ điểm A đến mặt phẳng (ABC) bằng
a
5
2
. Tính theo a thể tích V của khối lăng trụ ABC.ABC.
A
.
V
125
3
96...
Đọc tiếp
Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng A'B với mặt phẳng (ABC) bằng 60 0 và khoảng cách từ điểm A đến mặt phẳng (A'BC) bằng a 5 2 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A . V = 125 3 96 a 3
B . V = 125 3 288 a 3
C . V = 125 3 384 a 3
D . V = 125 3 48 a 3
Đáp án A.
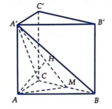
Gọi M là trung điểm của BC thì BC ⊥ (A'AM)
Từ A kẻ AH
⊥
A'M, 
Suy ra
Góc giữa đường thẳng A'B và mặt phẳng (ABC) bằng góc A ' M A ^
Theo giả thiết ta có A ' M A ^ = 60 0
Đặt AB = 2x 
Từ giả thiết ta có
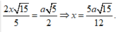
Do đó:
Vậy thể tích khối lăng trụ ABC.A'B'C' là V = 125 3 96 a 3
Phân tích phương án nhiễu.
Phương án B: Sai do HS tính đúng như trên nhưng nhớ nhầm công thức tính thể tích khối lăng trụ sang công thức tính thể tích khối chớp.
Cụ thể
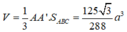
Phương án C: Sai do HS giải như trên và tìm được 
nhưng lại tính sai diện tích tam giác ABC. Cụ thể
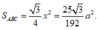
Do đó tính được
Phương án D: Sai do HS tính đúng như trên nhưng tính sai diện tích tam giác ABC. Cụ thể:
Do đó tính được V = 125 3 48 a 3
Đúng 0
Bình luận (0)