Cho (0) đường kinh AB,lấy M là 1 điểm thuộc (0) a) chứng minh tam giác AMB vuông b) Tiếp tuyến tại A của (0) cách BM tại K Gọi D là trang điểm của AK .chứng minh DM là tiếp tuyến của (0). c) Tiếp tuyến tại B của (0) cài DM tại E. Tính AD.BE theo R

Những câu hỏi liên quan
Cho đường tròn (O;R) đường kính AB. Lấy M bất kì trên cung AB sao cho AM > BM.
a) Chứng minh tam giác AMB vuông.
b) Tia tiếp tuyến Ax của (O) tại A cắt BM tại C.Tiếp tuyến tại M của (O) cắt tia Ax tại I. Chứng
minh IA=IC.
c) Kẻ MH⊥ AB(H AB). Gọi K là trung điểm của MH. Chứng minh B,K,I thẳng hàng.
d) Tia AK cắt IM tại D. Chứng minh BD là tiếp tuyến của (O).
a: Xét (O) có
ΔAMB nội tiếp đường tròn
AB là đường kính
Do đó: ΔAMB vuông tại M
Cho đường tròn (O;R) đường kính AB. Lấy M bất kì trên cung AB sao cho AM BM.a) Chứng minh tam giác AMB vuông.b) Tia tiếp tuyến Ax của (O) tại A cắt BM tại C.Tiếp tuyến tại M của (O) cắt tia Ax tại I. Chứngminh IAIC.c) Kẻ MH⊥ AB(H AB). Gọi K là trung điểm của MH. Chứng minh B,K,I thẳng hàng.d) Tia AK cắt IM tại D. Chứng minh BD là tiếp tuyến của (O)Giúp mình với, mình đang cần gấp
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Lấy M bất kì trên cung AB sao cho AM > BM.
a) Chứng minh tam giác AMB vuông.
b) Tia tiếp tuyến Ax của (O) tại A cắt BM tại C.Tiếp tuyến tại M của (O) cắt tia Ax tại I. Chứng
minh IA=IC.
c) Kẻ MH⊥ AB(H AB). Gọi K là trung điểm của MH. Chứng minh B,K,I thẳng hàng.
d) Tia AK cắt IM tại D. Chứng minh BD là tiếp tuyến của (O)
Giúp mình với, mình đang cần gấp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Cho đường tròn tâm O, đường kính AB. Lấy điểm M trên đường tròn (M
khác A và B). tiếp tuyến tại A của đường tròn ( O) cắt tia BM tại điểm C.
a) Chứng minh rằng ∆ AMB vuông và AB 2 = BC. BM
b) Gọi E là trung điểm của đoạn thẳng AC. Chứng minh rằng EM là tiếp
tuyến của của đường tròn (O)
Bài 148. Cho đường tròn (O) đường kính AB. Trên tiếp tuyến tại A của (O) lấy điểm M bất kì, BM cắt (O) tại C. Vẽ OD vuông góc với BC (D thuộc BC).
a) Chứng minh D là trung điểm của BC.
b) Gọi E là trung điểm của MA. Chứng minh EC là tiếp tuyến của (O).
Bài 7. Cho (O;5cm) đường kính BC, lấy điểm A thuộc (O) sao cho AB = 6cm. Tiếp tuyến tại B của (O) cắt
tia CA tại D.
a) Chứng minh tam giác ABC vuông và tính AC.
b) Qua O kẻ đường vuông góc với AB cắt BD tại M. Chứng minh MA là tiếp tuyến của (O)c) Gọi K là giao điểm của MC và (O). Chứng minh đường thẳng BK chứa tia phân giác của góc AKD
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=8(cm)
b: Xét ΔBOM và ΔAOM có
OB=OA
\(\widehat{BOM}=\widehat{AOM}\)
OM chung
Do đó: ΔBOM=ΔAOM
Suy ra: \(\widehat{OBM}=\widehat{OAM}=90^0\)
hay MA là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
. Cho tam giác ABC (AB AC) nội tiếp đường tròn (O) có BC là đường kính, vẽđường cao AH của tam giác ABC.H thuộc BCb) Tiếp tuyến tại A của đường tròn (O) cắt các tiếp tuyến tại B và C lần lượt tại M vàN. Chứng minh: MN MB + NC và0 MON 90 .c) Trên cạnh AC lấy điểm E sao cho AB AE. Gọi I là trung điểm của BE. Chứngminh 3 điểm M, I, O thẳng hàng.d) Chứng minh: HI là tia phân giác của góc AHCLàm mk câu cd thui nha
Đọc tiếp
. Cho tam giác ABC (AB <AC) nội tiếp đường tròn (O) có BC là đường kính, vẽ
đường cao AH của tam giác ABC.H thuộc BC
b) Tiếp tuyến tại A của đường tròn (O) cắt các tiếp tuyến tại B và C lần lượt tại M và
N. Chứng minh: MN = MB + NC và
0 MON 90 .
c) Trên cạnh AC lấy điểm E sao cho AB = AE. Gọi I là trung điểm của BE. Chứng
minh 3 điểm M, I, O thẳng hàng.
d) Chứng minh: HI là tia phân giác của góc AHC
Làm mk câu cd thui nha
Cho đường tròn (O; R) có đường kính AB. Bán kính CO vuông góc với AB. M là một điẻm bất kỳ trên cung nhỏ AC (M khác A, C), BM cắt AC tại H. Gọi K là hình chiếu của H trên ABa, Chứng minh CBKH là tứ giác nội tiếpb, Chứng minh:
A
C
M
^
A
C
K
^...
Đọc tiếp
Cho đường tròn (O; R) có đường kính AB. Bán kính CO vuông góc với AB. M là một điẻm bất kỳ trên cung nhỏ AC (M khác A, C), BM cắt AC tại H. Gọi K là hình chiếu của H trên AB
a, Chứng minh CBKH là tứ giác nội tiếp
b, Chứng minh: A C M ^ = A C K ^
c, Trên đoạn thẳng BM lấy điểm E sao cho BE = AM. Chứng minh tam giác ECM là tam giác vuông cân tại C
d, Gọi d là tiếp tuyến của (O) tại điểm A; cho P là điểm nằm trên d ao cho hai điểm P, C nằm trong cùng một nưanr mặt phẳng bờ AB và A P . M B M A = R . Chứng minh đường thẳng PB đi qua trung điểm của đoạn thẳng HK
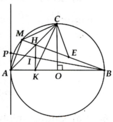
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)
Đúng 2
Bình luận (0)
cho nửa đường tròn tâm O đường kính AB đường thẳng với AB tại O cắt nửa đường tròn tại C.kẻ tiếp tuyến Bt với nửa đường tròn,AC cắt tiếp tuyến tại I.a) chứng minh rằng tam giác ABI vuông cân.b) lấy D là một điểm trên cung BC,gọi J là giao điểm của AD với tiếp tuyến Bt.chứng minh rằng tứ giác JDCI nội tiếp đường tròn.c) chứng minh rằng AC.AIAD.AJd) tiếp tuyến tại D của đường tròn cắt Bt tại K, hạ DH vuông góc với AB . chứng minh AK đi qua trung điểm của DH.LÀM GIÚP MK Ý d NHA MN...
Đọc tiếp
cho nửa đường tròn tâm O đường kính AB đường thẳng với AB tại O cắt nửa đường tròn tại C.kẻ tiếp tuyến Bt với nửa đường tròn,AC cắt tiếp tuyến tại I.
a) chứng minh rằng tam giác ABI vuông cân.
b) lấy D là một điểm trên cung BC,gọi J là giao điểm của AD với tiếp tuyến Bt.chứng minh rằng tứ giác JDCI nội tiếp đường tròn.
c) chứng minh rằng AC.AI=AD.AJ
d) tiếp tuyến tại D của đường tròn cắt Bt tại K, hạ DH vuông góc với AB . chứng minh AK đi qua trung điểm của DH.
LÀM GIÚP MK Ý d NHA MN...













