tính chu vi hình bình hành. BiêtAB=3cm, BC=5cm

Những câu hỏi liên quan
Hình bình hành ABCD có độ dài 2 cạnh liên tiếp AB=3cm, BC=2cm thì có chu vi là: A.5cm B.6cm C.12cm D.10cm
Hình bình hành ABCD có cạnh AB = 8cm, cạnh BC = 5cm và chiều cao AH = 4cm. Tính chu vi, diện tích hình bình hành đó (vẽ hình )
Chu vi hình bình hành là:
\(\left(8+5\right)\times2=13\times2=26\left(cm\right)\)
Diện tích hình bình hành là:
\(8\times4=32\left(cm^2\right)\)
Đúng 2
Bình luận (0)
C=(AB+BC)*2=26cm
S=4*8=32cm2
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có AB = 18cm, BC = 6cm và chiều cao AH = 5cm (như hình vẽ). Hãy tính chu vi và diện tích của hình bình hành ABCD.
Tính chu vi và diện tích hình bình hành ABCD biết AB = 9m, BC = 5cm,
AH = 4cm
\(C=\left(AB+BC\right)\cdot2=\left(9+5\right)\cdot2=28\left(cm\right)\)
\(S=4\cdot9=36\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Hình bình hành ABCD có độ dài cạnh AB là a, độ dài cạnh BC là b.Công thức tính chu vi P của hình bình hành là.P (a +b) x 2(a và b cùng một đơn vị đo)Áp dụng công thức trên để tính chu vi hình bình hành, biết :a) a 8cm; b 3cm;b) a 10dm; b 5dm.
Đọc tiếp
Hình bình hành ABCD có độ dài cạnh AB là a, độ dài cạnh BC là b.
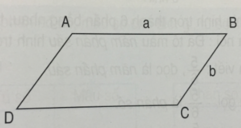
Công thức tính chu vi P của hình bình hành là.
P (a +b) x 2
(a và b cùng một đơn vị đo)
Áp dụng công thức trên để tính chu vi hình bình hành, biết :
a) a = 8cm; b = 3cm;
b) a= 10dm; b= 5dm.
Muốn tính chu vi hình bình hành ta lấy tổng độ dài hai cạnh liên tiếp nhân với 2 ( cùng một đơn vị đo).
Đáp án :
a) Nếu a =8 cm; b= 3cm thì P = ( 8 + 3 ) x 2 = 22 cm
b) Nếu a= 10dm ; b= 5dm thì P =( 10 + 5) x 2 = 30dm.
Đúng 0
Bình luận (0)
Hình bình hành ABCD có độ dài cạnh AB là a, độ dài cạnh BC là b.Công thức tính chu vi P của hình bình hành là.P (a +b) x 2(a và b cùng một đơn vị đo)Áp dụng công thức trên để tính chu vi hình bình hành, biết :a) a 8cm; b 3cm;b) a 10dm; b 5dm.
Đọc tiếp
Hình bình hành ABCD có độ dài cạnh AB là a, độ dài cạnh BC là b.
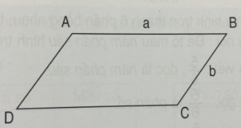
Công thức tính chu vi P của hình bình hành là.
P (a +b) x 2
(a và b cùng một đơn vị đo)
Áp dụng công thức trên để tính chu vi hình bình hành, biết :
a) a = 8cm; b = 3cm;
b) a= 10dm; b= 5dm.
a) Nếu a =8 cm; b= 3cm thì P = ( 8 + 3 ) x 2 = 22 cm
b) Nếu a= 10dm ; b= 5dm thì P =( 10 + 5) x 2 = 30dm.
Đúng 0
Bình luận (0)
1. cho hình bình hành ABCD, M và N lần lượt là trung điểm của AB và CD. Chứng minh các tứ giác AMCN và MBND là hình bình hành
2.Cho tam giác ABC có AB=3cm, AC=5cm. Các điểm M,N,P lần lượt là trung điểm của AB,AC và BC
a, Chứng minh tứ giác BMNP là hình bình hành
b,Tính chu vi của tứ giác BMNP nếu góc B=90 độ
1.
AB=CD (cặp cạnh đối hbh)
AM=AB/2 và CN=CD/2
=> AM=CN (1)
AM thuộc AB; CN thuộc CD mà AB//CD => AM//CN (2)
Từ (1) và (2) => AMCN là hbh(Tứ giác có một cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
2.
a. M là trung điểm AB; N là trung điểm AC => MN là đường trung bình của tgABC
=> MN//BC => MN//BP và MN=BP=BC/2
=> BMNP là hbh (lý do như bài 1)
b. Ta có BMNP là hbh và ^B=90 => BMNP là HCN
\(BC=\sqrt{AC^2-AB^2}=\sqrt{5^2-3^2}=4cm.\)
Từ kq câu a => MN=BC/2=4/2=2 cm
C/m tương tự câu a có NP là đường trung bình của tg ABC => NP=AB/2=3/2=1,5 cm
Chu vi BMNP là
(2+1,5)x2=7 cm
1.Cho hình thoi ABCD có diện tích là 96m2 có đường chéo ngắn là BD và đường chéo dài là AC .Biết BD 3/4 AC.Tính chu vi hình thoi ABCD.2.Một hình bình hành có diện tích là 40cm2.Biết độ dài cạnh đáy gấp đôi cạnh còn lại và gấp 2,5 lần chiều cao.Tính chu vi hình bình hành.3.Một mảnh đất hình bình hành có đáy 30m và khoảng cách giữa 2 cạnh bên là 24m.Người ta mở rộng mảnh đất bằng cách tăng mỗi đáy thêm 4m để được mảnh đất mới có diện tích hơn hình bình hành ban đầu là 48m2.Tính chu vi hình bình hà...
Đọc tiếp
1.Cho hình thoi ABCD có diện tích là 96m2 có đường chéo ngắn là BD và đường chéo dài là AC .Biết BD =3/4 AC.Tính chu vi hình thoi ABCD.
2.Một hình bình hành có diện tích là 40cm2.Biết độ dài cạnh đáy gấp đôi cạnh còn lại và gấp 2,5 lần chiều cao.Tính chu vi hình bình hành.
3.Một mảnh đất hình bình hành có đáy 30m và khoảng cách giữa 2 cạnh bên là 24m.Người ta mở rộng mảnh đất bằng cách tăng mỗi đáy thêm 4m để được mảnh đất mới có diện tích hơn hình bình hành ban đầu là 48m2.Tính chu vi hình bình hành ban đầu.
4.Hình bình hành ABCD có AB=6cm;BC=4cm.Gọi M,N,P,Q lần lượtlà trung điểm của các cạnh AB,BC,DC,AD.Nối MP,QN.Hỏi hình vẽ được có tất cả bao nhiêu hình bình hành?Tính tổng chu vi của tất cả các hình bình hành đó.
5.Một hình bình hành có chu vi 36cm, cạnh ngắn bằng khoảng cách giữa hai cạnh dài và bằng nửa cạnh dài.Tính diện tích hình bình hành.
6.Một hình bình hành có chu vi 64cm,khoảng cách giữa 2 cạnh ngắn là 9cm,khoảng cách giữa 2 cạnh dài là 3cm tính diện tích hình đó
7.Một hình bình hành có chu vi gấp 3 lần cạnh dài,độ dài cạnh ngắn là 4cm,khoảng cách giữa 2 cạnh dài là 5cm. Tính chu vi,diện tích hình đó
GIẢI CHI TIẾT GIÚP MÌNH NHA
Diện tích hình bình hành bằng 24 c m 2 . Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2cm và 3cm. Tính chu vi của hình bình hành.
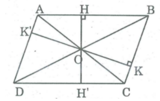
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.
S
A
B
C
D
= HH'.AB ⇒ ![]()
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
S
A
B
C
D
= KK'.AB ⇒ ![]()
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).
Đúng 0
Bình luận (0)

















