cho tam gíac abc vuông tại a m là tđ của bc ;ấy điểm d sao cho m là tđ của ad a) chứng minh abcd là hình chữ nhật b kẻ ah vuông góc với bc trên ah lấy e sao cho ah=he chứng minh ae vuông góc ed

Những câu hỏi liên quan
Cho tam gíac ABC vuông tại A, M là trung điểm của BC, H là hình chiếu của M trên AC, K là hình chiếu của H trên BC. Tính diện tích tam giác ABC biết MH=15mm, HK=12mm
Cho tam gíac ABC. Vẽ phía ngoài tam gíac các hình vuông ABDE, ACFG, BCMN. Đường cao AH của tam gíac ABC cắt MN tại K. Tính diện tích ABC lớn nhất với BC = a
cho tam gíac abc cân ở a gọi i và m là tđ của ac và bc a)trên tia mi lấy điểm k sao cho mi=ik chứng minh makc là hình chữ nhật b)chứng minh bamk là hình bình hành c) chứng minh aimb là hình thang d) gọi q là tđ của am chứng minh b,q,k thẳng hàng
a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Hình bình hành AMCK có \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: ta có: AMCK là hình chữ nhật
=>AK//CM và AK=CM
Ta có: AK//CM
M\(\in\)BC
Do đó: AK//MB
Ta có: AK=CM
MB=MC
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
c: ta có: ABMK là hình bình hành
=>MK//AB
=>MI//AB
Xét tứ giác AIMB có MI//AB
nên AIMB là hình thang
d: Ta có: ABMK là hình bình hành
=>AM cắt BK tại trung điểm của mỗi đường
mà Q là trung điểm của AM
nên Q là trung điểm của BK
=>B,Q,K thẳng hàng
Đúng 1
Bình luận (0)
a) Để chứng minh MAKC là hình chữ nhật, ta cần chứng minh rằng các cạnh MA và KC vuông góc và có độ dài bằng nhau.Vì tam giác ABC cân ở A, nên ta có AM = CM. Vì M là trung điểm của AC, nên ta có AM = MC.Vì MI = IK (theo đề bài), và M là trung điểm của AC, nên ta có AI = IC.Do đó, ta có AM = MC = AI = IC.Vậy, ta có MA = KC và MA vuông góc KC.Từ đó, ta có thể kết luận rằng MAKC là hình chữ nhật.b) Để chứng minh BAMK là hình bình hành, ta cần chứng minh rằng các cạnh BA và MK song song và có độ dài bằng nhau.Vì MI = IK (theo đề bài), và M là trung điểm của AC, nên ta có AI = IC.Vì tam giác ABC cân ở A, nên ta có BA = BC.Vì M là trung điểm của AC, nên ta có BM = MC.Vậy, ta có BA = BC và BM = MC.Từ đó, ta có thể kết luận rằng BAMK là hình bình hành.c) Để chứng minh AIMB là hình thang, ta cần chứng minh rằng các cạnh AI và BM song song.Vì MI = IK (theo đề bài), và M là trung điểm của AC, nên ta có AI = IC.Vì M là trung điểm của AC, nên ta có BM = MC.Vậy, ta có thể kết luận rằng AIMB là hình thang.d) Để chứng minh B, Q, và K thẳng hàng, ta cần chứng minh rằng các điểm B, Q, và K nằm trên cùng một đường thẳng.Vì M là trung điểm của AC, nên ta có MQ là đường trung tuyến của tam giác ABC. Do đó, MQ song song với BC.Vì MI = IK (theo đề bài), và M là trung điểm của AC, nên ta có AI = IC.Vậy, ta có thể kết luận rằng B, Q, và K thẳng hàng.
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a.vẽ am vuông góc bc tại m
a)c/m tam giác acm=tam giác abm
b)gọi n là tđ ab.đường thẳng qua a song song vs bc cắt mn tại e.c/mbv=2ae
c)gọi o là tđ của am,c/m e,o,c thẳng hàng
Giải giúp mik câu b,c vs ạ.Thks
b/ Có AE // BC (GT)
=> \(\widehat{EAN}=\widehat{ABC}\)
Xét t/g EAN và t/g MBN có
\(\widehat{EAN}=\widehat{ABC}\) (cmt(AN = BN (GT)
\(\widehat{ENA}=\widehat{MNB}\) (đối đỉnh)
=> t/g EAN = t/g MBN (g.c.g)
=> AE = MB
Mà CM = BM (do t/g ABM = t/g ACM) ; M thuộc BC)
=> M là trung điểm BC=> 2AE = 2 MN=BC
c/ Có
AM ⊥ BC (GT)AE // BC
=> AM ⊥ AE
=> \(\widehat{EAO}=\widehat{OMC}=90^o\)
Xét t/g EAO và t/g CMO có
EA = CM (=BM)\(\widehat{EAO}=\widehat{OMC}=90^o\)
AO = MO
=> t/g EAO = t/g CMO (c.g.c)=> \(\widehat{EOA}=\widehat{COM}\)
Mà 2 góc này đối đỉnh
=> E , O , C thẳng hàng.
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông cân tại A, từ A kẻ đường thẳng d nằm ngoài tam giác ABC, kẻ BD vuông góc với d, CE cũng vuông góc với d; gọi M là TĐ của BC. CMR tam giác MDE vuông cân.
cho tam giác ABC vuông tại A có AB = AC . Gọi M là TĐ của BC, D là TĐ của AC
a, CMR, AM vuông góc vs BC
b, Tù A kẻ đường thẳng vuông góc vs BD cắt BC tại E. Trên tia đối tia DE lấy đ' F sao cho DF = DE . CMR, AE//CE
c, Từ C dựng đường thẳng vuông góc vs AC cắt AE tại G . CMR : tam giác BAD = tam giác ACG
d, CM, AB = 2CG
â)xét tam giác AMBvà tam giác AMC
AB=AC( gt)
AM chung
MB=MC ( M là trung điểm của BC )
=> tam giác AMB= tam giác AMC ( c.c.c)
=> góc AMB= góc AMC ( 2 góc tương ứng )
mà góc AMB+ góc AMC = 180O ( 2 GÓC KỀ BÙ )
=> góc AMB= góc AMC=90O
=> AM vuông góc với BC
b) xét tam giác ADF và tam giác ADE
DF=DE ( gt)
góc ADF= góc CDE ( 2 góc đối đỉnh )
AD=CD ( D là trung điểm của AC)
=> tam giác ADF = tam giác ADE ( c.g.c)
=> góc CAF= góc ACÊ ( 2 góc tương ứng ) mà chúng ở vị trí so le trong do AC cắt AF và CE
=.> AF// CE
Đúng 0
Bình luận (0)
Cho Tam giác ABC góc A<90 độ. Vẽ ra phía ngoài tam giác đó 2 tam giác vuông cân tại A. Gọi M là TĐ của DE. CMR MA vuông góc với BC
tam giác abc vuông tại a.H là tđ BC .kẻ HN vuông góc AC ,HM vuông góc AB
a)CM tg AMHN là hình chữ nhật
b) lấy E đối xứng Hqua M,tg AHPE là hình k ví sao
c)lấy Fđối xứng H qua N tg AHCF là hình j vì sao
bài 2 :cho tg ABC vuông tại A .K là tđ BC. kể KM vuông góc AB,KN vuông góc AC
a) cm tg AMKN là hình chữ nhật
b)lấy E đối xứng vs K qua M. tg AKBE là hình j vì sao
c) lấy F đối xứng vs K qua N .cm BE //CF và BECF. Vẽ hình giúp mik luôn nha
Đọc tiếp
tam giác abc vuông tại a.H là tđ BC .kẻ HN vuông góc AC ,HM vuông góc AB a)CM tg AMHN là hình chữ nhật b) lấy E đối xứng Hqua M,tg AHPE là hình k ví sao c)lấy Fđối xứng H qua N tg AHCF là hình j vì sao bài 2 :cho tg ABC vuông tại A .K là tđ BC. kể KM vuông góc AB,KN vuông góc AC a) cm tg AMKN là hình chữ nhật b)lấy E đối xứng vs K qua M. tg AKBE là hình j vì sao c) lấy F đối xứng vs K qua N .cm BE //CF và BE=CF. Vẽ hình giúp mik luôn nha
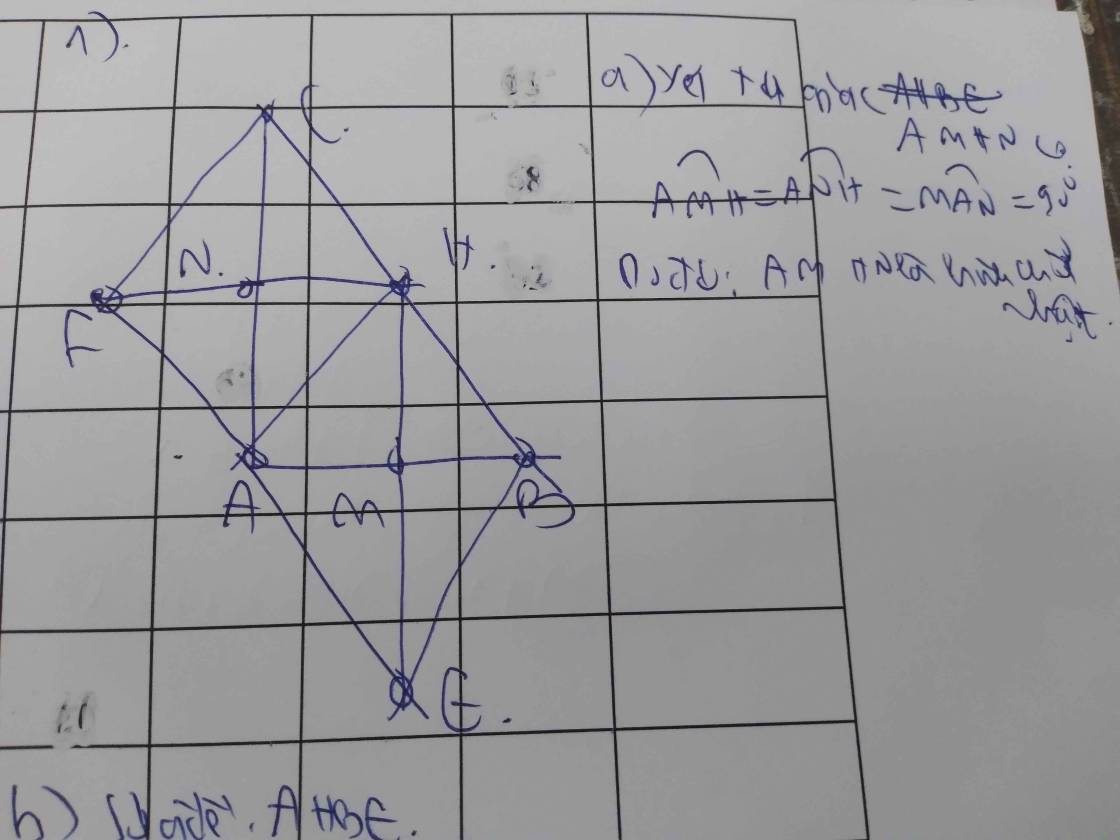
Cho tam giác ABC vuông cân tại A, M là TĐ của BC, N thuộc BC. Kẻ BD, CE vuông góc với AN tại D và E
a. Tam giác ABM, ACM là tam giác gì
b. CM tam giác ABD= tam giác CAE
c. MDE là tam giác gì