Cho tam giác ABC có AB < AC, AK là đường cao. Gọi N là trung điểm AC, Lấy F sao cho N là trung điểm KF.
a) cminh AKCF là hcn
b) vẽ NT vuông góc với CF, lấy E sao cho T là trung điểm NE. Cminh NCEF là hình thoi.
c) AT cắt NF tại Q. Cminh AC = 6QN.

Những câu hỏi liên quan
Cho tam giác ABC có AB < AC, AK là đường cao. Gọi N là trung điểm AC, Lấy F sao cho N là trung điểm KF.
a) cminh AKCF là hcn
b) vẽ NT vuông góc với CF, lấy E sao cho T là trung điểm NE. Cminh NCEF là hình thoi.
c) AT cắt NF tại Q. Cminh AC = 6QN.
mọi người giải hộ mình với mình đang cần gấp .-.
Cho tam giác ABC có góc ACB = 90 độ. Gọi M là trung điểm của AB. Trên tia đối của tia MC lấy N sao cho MC=NM a) Cminh tam giác ANM= tam giác BCM b) Cminh BN song song với AC c) Cminh NA vuông góc với AC d) Vẽ E thuộc BN , F thuộc AC sao cho BE=AF.Cminh M là trung điểm của EF
Cho tgiac ABC vuông tại A(ABAC), vẽ đường cao AH. Trên đoạn thẳng HC lấy điểm M (M ko trùng với H và C), từ M vẽ MN vuông góc với AC tại N.a. CMinh tgiac CMM đồng dạng với tam giác CAH và CA.CNCH.CMb. CMinh tgiac AMC đồng dạng với tgiac HNCc. Trên tia đối tia AC lấy điểm D sao cho ADAC. Vẽ AE vuông góc với BD tại E . Cminh rằng góc BEHgóc BCNd. Gọi K,F lần lượt là trung điểm của BH và BD.I là giao điểm của EK và CF. CMinh rằng KC.IEEF.IC
Đọc tiếp
Cho tgiac ABC vuông tại A(AB<AC), vẽ đường cao AH. Trên đoạn thẳng HC lấy điểm M (M ko trùng với H và C), từ M vẽ MN vuông góc với AC tại N.
a. CMinh tgiac CMM đồng dạng với tam giác CAH và CA.CN=CH.CM
b. CMinh tgiac AMC đồng dạng với tgiac HNC
c. Trên tia đối tia AC lấy điểm D sao cho AD<AC. Vẽ AE vuông góc với BD tại E . Cminh rằng góc BEH=góc BCN
d. Gọi K,F lần lượt là trung điểm của BH và BD.I là giao điểm của EK và CF. CMinh rằng KC.IE=EF.IC
Cho tam giác ABC. Lấy điểm I nằm trong tam giác sao cho góc IBA = IBC. Gọi P là trung điểm BI. H là trung điểm CI. K là trung điểm BC. Vẽ IE vuông góc AB, IF vuông góc với AC
a. Cminh PIHK là hình bình hành
b. Cminh tam giác EFK là tam giác cân
Cho tam giác ABC, trên AB, Ac lấy điểm D,E sao cho BD=CE. Gọi M,N,I,K thứ tự là trung điểm của BE, CD, DE, BC:
a, Cminh: MN vuông góc IK
b, Cminh: tia phân giác góc BAC song song với IK
c, Gọi P,Q là giao của M,N với AB, AC. Cminh: AP= AQ
cho tam giác ABC cân tại A, gọi M là trung điểm của BC.
B) Vẽ BE vuông góc với với AC tại E, CF vuông góv AB tại F. CM: AE=AF c) Trên tia AM lấy điểm K bất kì sao cho AM<AK CM: AC-AF>KF-KC
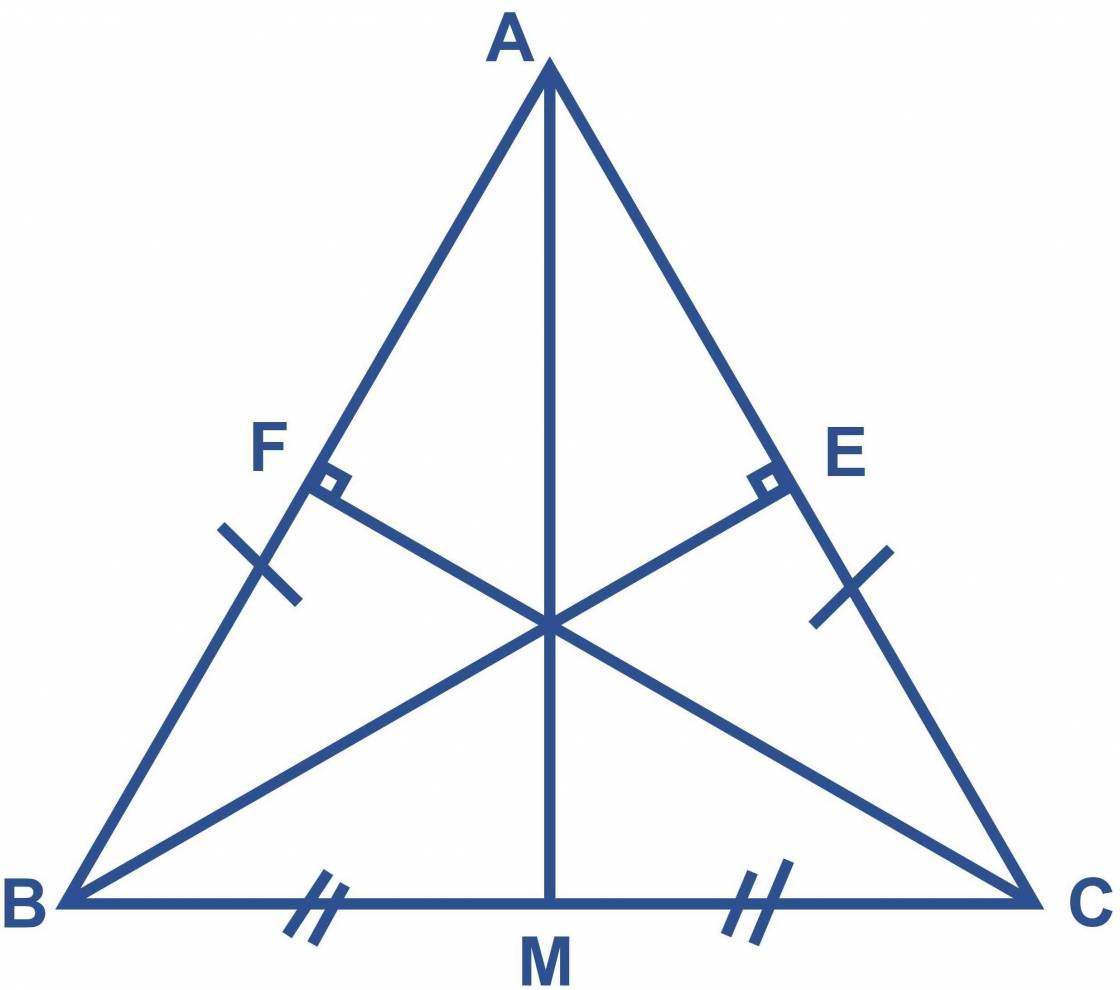
b) xét ΔBEA và ΔCFA, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
\(\widehat{A}\) là góc chung
=> ΔBEA = ΔCFA (ch-gn)
=> AE = AF (2 cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn,đường cao AH.Kẻ HE vuông góc với AB,trên tia HE lấy điểm M sao cho E là trung điểm của HM.Kẻ HF vuông góc với AC ,trên tia HF lấy điểm N sao cho F là trung điểm của HN.CMR
a) tam giác AMN cân
b) EF//MN
c)Gọi I là trung điểm của MN.CMR:AI vuông góc với EF
d) góc MAN=2.BAC
a, Vì AE là vừa là đg cao (AE⊥HM) vừa là trung tuyến nên tg AHM cân tại A
Do đó AH=AM
Vì AF là vừa là đg cao (AF⊥HN) vừa là trung tuyến nên tg AHN cân tại A
Do đó AH=AN
Từ đó ta được AM=AN hay tg AMN cân tại A
b, Vì E,F là trung điểm HM,HN nên EF là đtb tg MHN
Do đó EF//MN
c, Vì AI là trung tuyến tg AMN cân tại A nên AI cũng là đg cao
Do đó AI⊥MN
Mà EF//MN nên AI⊥EF
d, Vì tg AEH và tg AFH cân tại A nên AE,AF lần lượt là p/g \(\widehat{MAH}\) và \(\widehat{NAH}\)
Do đó \(\widehat{MAN}=\widehat{MAH}+\widehat{NAH}=2\cdot\widehat{EAH}+2\cdot\widehat{FAH}=2\cdot\widehat{BAC}\)
Đúng 2
Bình luận (0)
Cho tam cho tam giác ABC có góc A = 90 độ Gọi M là trung điểm AC N là trung điểm AB Trên tia BM lấy điểm E sao cho M là trung điểm BE Trên tia CN lấy điểm F sao cho N là trung điểm CF Chứng minh : a) AE = AF b) 3 điểm A, E, F thẳng hàng
cho tam giác ABC vuông tại A. Gọi điểm M, N lần lượt là trung điểm của AB và AC. Qua M vẽ đường thẳng a vuông góc với AB tại M. Qua N vẽ đường thẳng b vuông góc với AC tại N. Đường thẳng a cắt đường thẳng b tại D. Trên a lấy E sao cho M là trung điểm của DE. Trên đường thẳng b lấy F sao cho N là trung điểm của DF. Chứng minh rằng:a) AE AF.b) 3 điểm E,A,F thẳng hàng.c) A là trung điểm của EF.
Đọc tiếp
cho tam giác ABC vuông tại A. Gọi điểm M, N lần lượt là trung điểm của AB và AC. Qua M vẽ đường thẳng a vuông góc với AB tại M. Qua N vẽ đường thẳng b vuông góc với AC tại N. Đường thẳng a cắt đường thẳng b tại D. Trên a lấy E sao cho M là trung điểm của DE. Trên đường thẳng b lấy F sao cho N là trung điểm của DF. Chứng minh rằng:
a) AE = AF.
b) 3 điểm E,A,F thẳng hàng.
c) A là trung điểm của EF.












