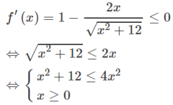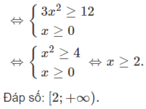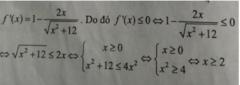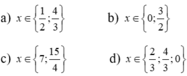-2x2+x+12=0

Những câu hỏi liên quan
Cho E = {x ≤ Z||x| ≤ 5}, F = {x ∈ N ||x| ≤ 5} và
B = {x ∈ Z|(x – 2)(x + 1)(2x2 – x – 3) = 0}. Chứng minh A ⊂ E và B⊂E
Cho A = {x ∈ R | x2+ x – 12 = 0 và 2x2 – 7x + 3 = 0}
B = {x ∈ Z | 3x2 – 13x + 12 =0 hoặc x2 – 3x = 0}
Tìm số nguyên x biết:
a) 12-(2x2-3)=7
b) 3x2-12=2x2+4
c) 2x-3.(2x+1)=4x-5.(x-3)
d) (x-2).(x+5)=0
Làm 1 câu bất kì cũng dc ạ!
a, 12 - (2\(x^2\) - 3) = 7
2\(x^2\) - 3 = 12 - 7
2\(x^2\) - 3 = 5
2\(x^2\) = 8
\(x^2\) = 4
\(\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a) \(12-\left(2x^2-3\right)=7\\ 12-2x^2+3=7\\ 15-2x^2=7\\ 2x^2=15-7=8\\ x^2=8:2=4\\ x=\pm2\)
b) \(3x^2-12=2x^2+4\\ 3x^2-2x^2=12+4\\ x^2=16\\ x=\pm4\)
Đúng 0
Bình luận (0)
b, 3\(x^2\) - 12 = 2\(x^2\) + 4
3\(x^2\) - 2\(x^2\) = 12 + 4
\(x^2\) = 16
\(\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình: 2 x 2 + x - 4 2 - 2 x - 1 2 = 0
(2x2 + x – 4)2 – (2x – 1)2 = 0
⇔ (2x2 + x – 4 – 2x + 1)(2x2 + x – 4 + 2x – 1) = 0
⇔ (2x2 – x – 3)(2x2 + 3x – 5) = 0
⇔ 2x2 – x – 3 = 0 (1)
hoặc 2x2 + 3x – 5 = 0 (2)
+ Giải (1): 2x2 – x – 3 = 0
Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.
+ Giải (2): 2x2 + 3x – 5 = 0
Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.
Vậy phương trình có tập nghiệm 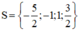
Đúng 0
Bình luận (0)
Cho hàm số f ( x ) = x - 2 x 2 + 12 . Giải bất phương trình f'(x) ≤ 0.
Câu 12. Cho các đa thức: f(x) = x3 - 2x2 + 3x + 1
g(x) = x3 + x - 1
h(x) = 2x2 - 1
a) Tính: f(x) - g(x) + h(x)
b) Tìm x sao cho f(x) - g(x) + h(x) = 0
\(\text{a)}f\left(x\right)-g\left(x\right)+h\left(x\right)=\left(x^3-2x^2+3x+1\right)-\left(x^3+x-1\right)+\left(2x^2-1\right)\)
\(=x^3-2x^2+3x+1-x^3-x+1+2x^2-1\)
\(=\left(x^3-x^3\right)+\left(-2x^2+2x^2\right)+\left(3x-x\right)+\left(1+1-1\right)\)
\(=2x+1\)
\(\text{b)Vì f(x)-g(x)+h(x)=0}\)
\(\Rightarrow2x+1=0\)
\(\Rightarrow2x\) \(=0-1=-1\)
\(\Rightarrow\) \(x\) \(=\left(-1\right):2=\dfrac{-1}{2}\)
\(\text{Vậy x=}\dfrac{-1}{2}\text{ thì f(x)-g(x)+h(x)=0}\)
Đúng 2
Bình luận (0)
a: \(f\left(x\right)-g\left(x\right)+h\left(x\right)\)
\(=2x^3-2x^2+4x+2x^2-1=2x^3+4x-1\)
b: f(x)-g(x)+h(x)=0
\(\Leftrightarrow2x^3+4x-1=0\)
\(\Leftrightarrow x\simeq0,2428\)
Đúng 0
Bình luận (0)
a) f(x) - g(x) + h (x) = x3 - 2x2 + 3x + 1 - (x3 + x - 1 ) + (2x2 - 1 )
= x3 - 2x2 + 3x + 1 - x3 - x + 1 + 2x2 - 1
= (x3 - x3) + ( -2x2 + 2x2) + (3x - x) + (1+1 - 1)
= 2x + 1
b) Đặt 2x + 1 = 0
=> 2x = -1
=> x = -1/2
Đúng 1
Bình luận (0)
Cho tập số f ( x ) = x - 2 x 2 + 12 Tập nghiệm của bất phương trình f'(x)≤0 là:
A. (-∞;2)∪[2;+∞)
B. (-∞;2)
C. [2;+∞)
D. (2;+∞)
Giải các phương trình:
a
)
3
x
2
−
5
x
+
1
x
2
−
4...
Đọc tiếp
Giải các phương trình:
a ) 3 x 2 − 5 x + 1 x 2 − 4 = 0 b ) 2 x 2 + x − 4 2 − 2 x - 1 2 = 0
a)
3 x 2 − 5 x + 1 x 2 − 4 = 0 ⇔ 3 x 2 − 5 x + 1 = 0
hoặc x 2 – 4 = 0 ( 2 )
+ Giải (1): 3 x 2 – 5 x + 1 = 0
Có a = 3; b = -5; c = 1 ⇒ Δ = ( - 5 ) 2 – 4 . 3 = 13 > 0
Phương trình có hai nghiệm: 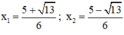
+ Giải (2): x 2 – 4 = 0 ⇔ x 2 = 4 ⇔ x = 2 hoặc x = -2.
Vậy phương trình có tập nghiệm 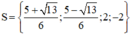
b)
2 x 2 + x − 4 2 − ( 2 x − 1 ) 2 = 0 ⇔ 2 x 2 + x − 4 − 2 x + 1 2 x 2 + x − 4 + 2 x − 1 = 0 ⇔ 2 x 2 − x − 3 2 x 2 + 3 x − 5 = 0 ⇔ 2 x 2 − x − 3 = 0 ( 1 )
hoặc 2 x 2 + 3 x – 5 = 0 ( 2 )
+ Giải (1): 2 x 2 – x – 3 = 0
Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.
+ Giải (2): 2 x 2 + 3 x – 5 = 0
Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.
Vậy phương trình có tập nghiệm 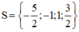
Đúng 0
Bình luận (0)
Cho biểu thức P 1+ 3/x2+5x+6 : ( 8x2/ 4x3-8x2 - 3x/ 3x2-12 -1/x+2)A) Rút gọn PB) Tìm các giá trị của x để P 0; P 1C) Tìm cã giá trị của x để P 0Cho biểu thứcQ (2x-x2/ 2x2 +8 - 2x2/ 3x3-2x2+4x-8) (2/x2 + 1-x/x)A) Rút gọn QB) Tìm giá trị nguyên của x để Q có giá trị nguyên
Đọc tiếp
Cho biểu thức P= 1+ 3/x2+5x+6 : ( 8x2/ 4x3-8x2 - 3x/ 3x2-12 -1/x+2)
A) Rút gọn P
B) Tìm các giá trị của x để P= 0; P= 1
C) Tìm cã giá trị của x để P> 0
Cho biểu thức
Q= (2x-x2/ 2x2 +8 - 2x2/ 3x3-2x2+4x-8) (2/x2 + 1-x/x)
A) Rút gọn Q
B) Tìm giá trị nguyên của x để Q có giá trị nguyên
Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
2
x
−
1
2
+
x
−
3
2
x
−
1
0
;
b)
3
−
2
x...
Đọc tiếp
Giải các phương trình sau:
a) 2 x − 1 2 + x − 3 2 x − 1 = 0 ;
b) 3 − 2 x 2 + 4 x 2 − 9 = 0 ;
c) 7 − x 2 + 2 3 x − 7 x − 3 = 0 ;
d) 4 3 x − 2 − 3 x − 2 3 = 0 .