
Giusp với ạ
Giusp e với ạ e cảm ơn ạ
Giusp mình với ạ


Giusp mình với ạ

Giusp mình với ạ !!

giusp mình với ạ
Giusp em với ạ
Bài 4:
Điện trở tương đương: \(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{40.60}{40+60}=24\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=I.R_{tđ}=0,5.24=12\left(V\right)\)
Cường độ dòng điện qua mỗi điện trở:
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{12}{40}=0,3\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{60}=0,2\left(A\right)\end{matrix}\right.\)
\(P=U.I=12.0,5=6\left(W\right)\)
\(A=P.t=6.1.60.60=21600\left(J\right)\)
Bài 5:
Điện trở tương đương của cả mạch: \(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{3.6}{3+6}=2\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=18V\)
Cường độ dòng điện qua mỗi điện trở và cả mạch:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{18}{2}=9\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{18}{3}=6\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{18}{6}=3\left(A\right)\end{matrix}\right.\)
Tiết diện của dây: \(R_2=\rho_2.\dfrac{l_2}{S_2}\Rightarrow S_2=\dfrac{\rho_2.l_2}{R_2}=\dfrac{1,6.10^{-6}.10}{6}\approx2,67.10^{-6}\left(m^2\right)\)
Giusp mình với ạ
Giusp em với ạ.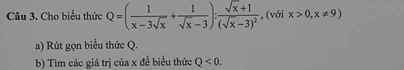
a) Với x>0,x\(\ne\)9
\(Q=\left(\dfrac{1}{x-3\sqrt{x}}+\dfrac{1}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-3\right)^2}=\left(\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}\right).\dfrac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
b)Với x>0,x\(\ne\)9
\(Q< 0< =>\dfrac{\sqrt{x}-3}{\sqrt{x}}< 0\)
\(< =>\sqrt{x}-3< 0\left(Vì\sqrt{x}>0\right)\)
\(< =>\sqrt{x}< 3\)
\(< =>x< 9\)
Kết hợp với ĐKXĐ ta được
0<x<9
Giusp mình với ạ!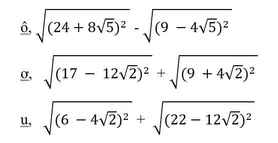
\(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}=24+8\sqrt{5}-9+4\sqrt{5}=15+12\sqrt{5}\)
\(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}=17-12\sqrt{2}+9+4\sqrt{2}=26-8\sqrt{2}\)
\(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}=6-4\sqrt{2}+22-12\sqrt{2}=28-16\sqrt{2}\)
\(ô,\\ \Rightarrow24+8\sqrt{5}-\sqrt{\left(9-4\sqrt{5}\right)^2}\\ \Rightarrow24+8\sqrt{5}-\left(9-4-\sqrt{5}\right)\\ \Rightarrow24+8\sqrt{5}-9+4\sqrt{5}\\ \Rightarrow15+8\sqrt{5}+4\sqrt{5}\\ \Rightarrow15+12\sqrt{5}\)
\(ơ,\\ g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4+\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+9+4\sqrt{2}\)
\(u,\\ 6-4\sqrt{2}+\sqrt{\left(22-12\sqrt{2}\right)}^2\\ \Rightarrow6-4\sqrt{2}+22-12\sqrt{2}\\ \Rightarrow28-4\sqrt{2}-12\sqrt{2}\\ \Rightarrow28-16\sqrt{2}\)
ô \(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}\)
= 24 + 8\(\sqrt{5}\) - 9 + 4\(\sqrt{5}\)
= 15 + 12\(\sqrt{5}\)
ơ \(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}\)
= 17 - 12\(\sqrt{2}\) + 9 + 4\(\sqrt{2}\)
= 26 - 8\(\sqrt{2}\)
u \(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}\)
= 6 - 4\(\sqrt{2}\) + 22 - 12\(\sqrt{2}\)
= 28 -16\(\sqrt{2}\)