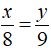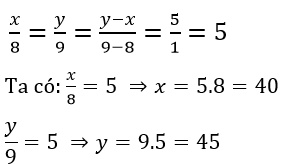Tìm độ dại ba cạnh của tam giác, biết chu vi của tam giác đó là 24m và độ dài ba cạnh tỉ lệ với các số 3,4,5
Trường có 3 lớp 7, biết 2/3 có số học sinh lớp 7A bằng 3/4 số học sinh lớp 7B và bằng 4/5 số học sinh lớp 7C. Lớp 7C có số học sinh ít hơn tổng số học sinh của 2 lớp kia là 57 bạn. Tính số học sinh mỗi lớp
Một miếng đất hình chữ nhật có chu vi bằng 70m . Tính diện tích của hình chữ nhật, biết tỉ số giữa hai cạnh của nó là 3/4
Làm guip mình ba bài này nhé đuk tick tất tick cho