b: MD*MC=MH*DC=2*a

a: Xet ΔBEC vuông tại B và ΔCFD vuông tại C có

BE=CF

BC=CD

=>ΔBEC=ΔCFD

=>góc BEC=góc CFD

=>góc CFD+góc FCM=90 độ

=>CE vuông góc BD

Xét ΔDMC vuông tại D và ΔCBE vuông tại B có

góc MCD=góc BEC

=>ΔDMC đồng dạng với ΔCBE

\(S_{CBE}=\dfrac{1}{2}\cdot S_{BAC}=\dfrac{1}{4}\cdot S_{ABCD}\)

ΔDMC đồng dạng với ΔCBE

=>\(\dfrac{S_{DMC}}{S_{CBE}}=\left(\dfrac{DC}{CE}\right)^2=\left(\dfrac{2\cdot BE}{\sqrt{\left(2\cdot BE\right)^2+BE^2}}\right)^2=\left(\dfrac{2}{\sqrt{5}}\right)^2=\dfrac{4}{5}\)

=>\(S_{DMC}=\dfrac{4}{5}\cdot S_{CBE}=\dfrac{4}{5}\cdot\dfrac{1}{4}\cdot S_{ABCD}=\dfrac{1}{5}\cdot S_{ABCD}\)

khó quá đi à

Đặt AM=x; AN=y

MN^2=AM^2+AN^2

=>\(MN=\sqrt{x^2+y^2}\)

\(P_{AMN}=AM+AN+MN=x+y+\sqrt{x^2+y^2}=2a\)

và x+y>=2*căn xy; \(\sqrt{x^2+y^2}>=\sqrt{2xy}\)

=>\(2a=x+y+\sqrt{x^2+y^2}>=2\sqrt{xy}+\sqrt{2xy}\)

=>\(2a>=\sqrt{xy}\left(2+\sqrt{2}\right)\)

=>\(\sqrt{xy}< =\dfrac{2a}{2+\sqrt{2}}\)

=>\(S_{AMN}=\dfrac{1}{2}xy< =\dfrac{1}{2}\cdot\left(\dfrac{2a}{2+\sqrt{2}}\right)^2=\left(3-2\sqrt{2}\right)a^2\)

Dấu = xảy ra khi \(x=y=\left(2-\sqrt{2}\right)a\)

Vì E thuộc cạnh AB nên EB < AB hay 2x < y

Ta có: AE = AB – EB = y – 2x (cm)

AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)

Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:

(y – 2x)(y + 3x) = y 2

Theo định lí Pitago, ta có: F C 2 = E B 2 + D G 2

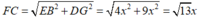
Chu vi ngũ giác ABCFG:

PABCFG = AB + BC + CF + FG + GA

= AB + BC + CF + FG + GD + DA

= y + y + x 13  + y – 2x + 3x + y = x(1 +  13 ) + 4y

Vì chu vi ngũ giác ABCFG bằng 100 + 4 13  (cm) nên ta có phương trình:

x(1 +  13  ) + 4y = 100 + 4 13

Ta có hệ phương trình:

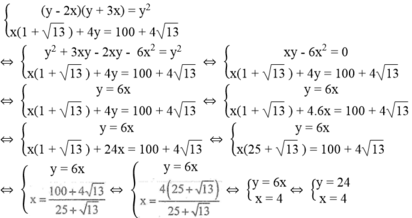
Giá trị của x và y thỏa điều kiện bài toán.

Vậy x = 4 (cm), y = 24 (cm).