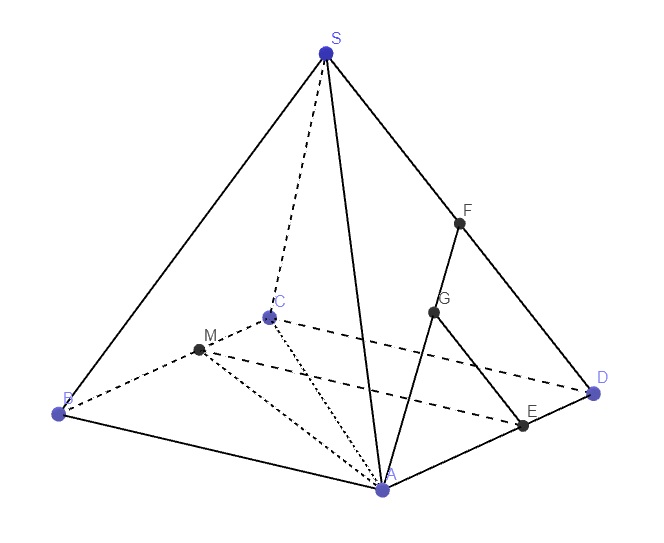
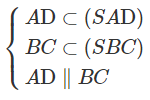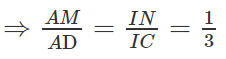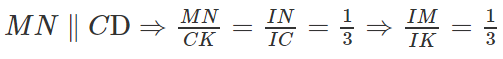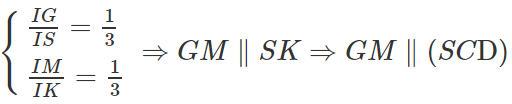cho hình chóp sabcd có đáy là hình bình hành, gọi G là trọng tâm tam giác SAD, gọi M thuộc cạnh cd hỏa mãn 3MD=CD. cmr MG//( SBC)

Những câu hỏi liên quan
Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm cuat CD, AD, SA thoả mãn MD=2MC, NA=3ND, PA=3PS. Gọi G là trọng tâm tam giác SBC
a) Tìm giao điểm K của BM và (SAC)
b) Chứng minh (NPK)//(SCD)
c) Chứng minh MG// (SAD)
Xem chi tiết
Bạn coi lại đề bài.
N,M,P,Q là các điểm trên CD, AD, SA hay trung điểm?
Vì nếu trung điểm thì làm sao thỏa mãn MD=2MC hay NA=3ND được?
Đúng 0
Bình luận (0)
cho hình chóp sabcd có đáy là hình bình hành, gọi G là trọng tâm tam giác SAD, gọi M thuộc cạnh cd hỏa mãn 3MD=CD. cmr MG//( SBC)
Gọi N là trung điểm AD
Trong mặt phẳng (ABCD), qua M kẻ đường thẳng song song BC cắt CN tại P \(\Rightarrow MP//BC//AD\) (1)
Áp dụng Talet: \(\frac{CP}{CN}=\frac{CM}{CD}=\frac{2}{3}\)
Trong tam giác SNC, ta có: \(\frac{SG}{NS}=\frac{CP}{NC}=\frac{2}{3}\Rightarrow GP//SC\) (Talet đảo) (2)
Từ (1); (2) \(\Rightarrow\left(MNG\right)//\left(SAC\right)\)
\(\Rightarrow MG//\left(SAC\right)\)
Đúng 0
Bình luận (1)
cho hình chóp s.abcd có đáy là hình bình hành . gọi g là trọng tâm của tam giác sad điểm m nằm trên đoạn dc sao cho dc=3dm
tìm giao tuyến (SAD) và (SBC)
tìm giao điểm K của đường thẳng BG và (SAC)
chứng minh rằng MG//(SBC)
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà 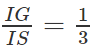
(G là trọng tâm của ∆SAB) nên
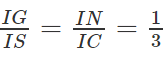
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy là hình bình hành ABCD. Gọi M,N là điểm trên BC,CD sao cho: CM=2BM , CN=2ND. Gọi G là trọng tâm tam giác SAD. +) Tìm giao tuyến của (GMN) và (SAD)
Cho hình chóp SABCD có đáy ABCD là hình bình hành. G, H lần lượt là trọng tâm tam giác SBC, tam giác SCD. Tìm giao tuyến (SGH) và (SAD)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a tất cả các cạnh bên đều bằng a. Gọi điểmM thuộc SD sao cho SD =3SM, G là trọng tâm của tam giác BCD gọi (a) là mặt phẳng chứa MG và song song với CD. Xác định và tính diện tích thiết diện của hình chóp với mp (a)
Xem chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của tam giác SAD và M là điểm thuộc cạnh BC sao cho GM// (SCD). Khi đó tỉ số diện tích của hai tam giác MAB và MAC là
Gọi F là trung điểm SD \(\Rightarrow\dfrac{GF}{GA}=\dfrac{1}{2}\) theo t/c trọng tâm
Trong mp (SAD), qua G kẻ đường thẳng song song SD cắt AD tại E
\(\Rightarrow GE||SD\Rightarrow GE||\left(SCD\right)\)
\(\left\{{}\begin{matrix}GM||\left(SCD\right)\\GE||\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow\left(GME\right)||\left(SCD\right)\Rightarrow ME||\left(SCD\right)\Rightarrow ME||CD\)
\(\Rightarrow CDEM\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow MC=ED\Rightarrow MB=EA\)
Áp dụng định lý Talet trong tam giác ADF: \(\dfrac{ED}{EA}=\dfrac{GF}{GA}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{MC}{MB}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{S_{MAB}}{S_{MAC}}=\dfrac{MB}{MC}=2\)
Đúng 2
Bình luận (1)
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành? A. AB3CD B. AB2CD C. CD2AB D. CD3AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp ![]() cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?

A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành? A. AB 3CD B. AB 2CD C. CD 2AB D. CD 3AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành?
A. AB = 3CD
B. AB = 2CD
C. CD = 2AB
D. CD = 3AB
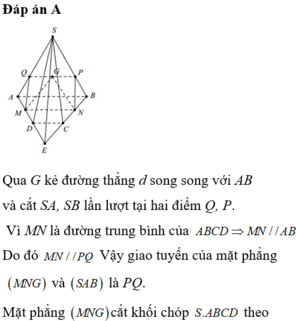
Đáp án A
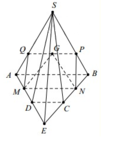
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB
Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.
Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Vì MN//PQ suy ra MNPQ là hình thang
Để MNPQ là hình bình hành ⇔ MN=PQ (1)
Gọi I là trung điểm của AB, G là trọng tâm tam giác S A B ⇒ S G S I = 2 3
Tam giác SAB có P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)
Mà MN là đường trung bình hình thang A B C D ⇒ M N = A B + C D 2 (3)
Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .
Đúng 1
Bình luận (0)