Cho tam giác MNP vuông tại m có MN = 3 cm góc b = 37 độ A giải tam giác vuông MNP ( số đo góc làm tròn đến độ) B: kẻ đường cao MH ( H€NP ) TÍNH MH Chứng minh góc nmh bằng góc P từ đó tính các tỉ số lượng góc của góc NMH
b: \(\widehat{NMH}+\widehat{N}=90^0\)
\(\widehat{P}+\widehat{N}=90^0\)
Do đó: \(\widehat{NMH}=\widehat{P}\)
1. Cho tam giác ABC vuông tại A, đường cao AH , AC= 3cm , HC= 1.8 cm
a) Giải tam giác ABC (tìm các góc và các cạnh còn lại của tam giác )
b) Tính độ dài phân giác AD của tam giác ABC ( số đo góc làm tròn đến phút , độ dài đoạn thẳng làm tròn đến số thập phân thứ 2)
2. Cho tam giác ABC nhọn , đường cao AH . Gọi M, N lần lượt là hình chiếu của H lên AB và AC .
CM: AM . AB = AN . AC
MÌNH CẦN GẤP TRONG TỐI NI
5, Tính các góc nhọn của 1 tam giác vuông, biết tỉ số giữa các cạnh góc vuông là 13:21( làm tròn đến phút)
2. Cạnh huyền của 1 tam giác vuông = 26cm . Độ dài của các cạnh góc vuông tỉ lệ với các số 2 và 3 . Tính các cạnh góc vuông. ( có vẽ hình )
3. CMR các tam giác mà có số đo của các cạnh tỉ lệ với các số 3,4,5 thì tam giác đó vuông
Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
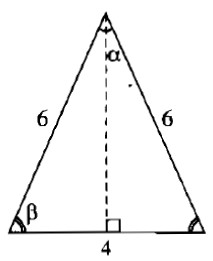
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.
Cho tam giác ABC vuông tại A, vẽ đường cao AH của tam giác ABC (H thuộc BC).
1) Nếu sin ACB = 3/5 và BC = 20 cm. Tính các cạnh AB, AC, BH và góc ACB (số đo góc làm tròn đến độ)
2) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D. Chứng minh: AD.AC = BH.BC.
3) Kẻ tia phân giác BE của DBA ( E thuộc đoạn DA). Chứng minh: tan EBA = AD/AB + BD
4) Lấy điểm K thuộc đoạn AC, Kẻ KM vuông góc với HC tại M, KN vuông góc với AH tại N. chứng minh : NH.NA+MH.MC=KA.KC
2: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBDC vuông tại B có BA là đường cao ứng với cạnh huyền DC
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)
a) Một tam giác vuông có cạnh huyền bằng 20 cm, độ dài các cạnh góc vuông tỉ lện với 3 và 4. Tính độ dài các cạnh góc vuông b) Tính các cạnh của một tam giác vuông biết tỉ số các cạnh góc vuông là 5:12, chu vi của tam giác bằng 60 cm
1) Một tam giác vuông có canh huyền là 5 và đường cao ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
2) Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3:4 và cạnh huyền là 125 cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.
câu 2
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5
1) Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5
Cho tam giác ABC vuông tại A có góc B = 60 độ
a)Tính số đo góc C và so sánh độ dài 3 cạnh của tam giác ABC.
b)Vẽ BD là tia phân giác của góc ABC (D thuộc AC). Qua D vẽ DK vuông góc với BC (K thuộc BC). Chứng minh tam giác BAD=tam giác BKD.
c)Chứng minh tam giác BDC cân và K là trung điểm BC.
d)Tia KD cắt BA tại I. Tính độ dài cạnh ID biết AB=3cm (làm tròn kết quả đến chữ số thập phân thứ nhất).
GIÚP MÌNH VỚI CÁC BẠN ƠI!!!
ARIGATO!!!
