CHO ĐƯỜNG TRÒN TÂM O BÁN KÍNH R VẼ CÁC ĐIỂM A,B,C,D THUỘC ĐƯỜNG TRÒN ĐÓ. TÌM GIÁ TRỊ LỚN NHẤT CỦA DIỆN TÍCH TỨ GIÁC ABCD THEO R

Những câu hỏi liên quan
cho các điểm A,B,C,D thuooch đường tròn tâm O bán kính R. tìm giá trị lớn nhất của \(S_{ABCD}\)
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
πcm
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
c
m
3
B.
60...
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 πcm . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho mặt cầu (S) bán kính R 5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
c
m
3
.
B. ...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3 .
B. 60 3 c m 3 .
C. 20 3 c m 3 .
D. 96 3 c m 3 .
Cho đường tròn tâm O, đường kính AB, M là một điểm thuộc nửa đường tròn. Qua M vẽ vẽ tiếp tuyến với nửa đường tròn, gọi D và C theo thứ tự là các hình chiếu vuông góc của A và B.a) Chứng minh M là trung điểm của CD b) Chứng minh AB BC + ADc) Giả sử góc AOM góc BOM. Từ B vẽ đường tròn vuông góc với BC, đường thẳng này cắt AD tại E. Chứng minh E thuộc nửa đường tròn tâm O d) Xác định vị trí của M trên 1/2 O sao cho tứ giác ABCD có diện tích lớn nhất và tính diện tích đó theo nửa bán kính rồi the...
Đọc tiếp
Cho đường tròn tâm O, đường kính AB, M là một điểm thuộc nửa đường tròn. Qua M vẽ vẽ tiếp tuyến với nửa đường tròn, gọi D và C theo thứ tự là các hình chiếu vuông góc của A và B.
a) Chứng minh M là trung điểm của CD
b) Chứng minh AB = BC + AD
c) Giả sử góc AOM > góc BOM. Từ B vẽ đường tròn vuông góc với BC, đường thẳng này cắt AD tại E. Chứng minh E thuộc nửa đường tròn tâm O
d) Xác định vị trí của M trên 1/2 O sao cho tứ giác ABCD có diện tích lớn nhất và tính diện tích đó theo nửa bán kính rồi theo 1/2 đường tròn đã cho.
Giúp em với ạ TvT
Cho nửa đường tròn (O) có tâm O và đường kính AB2R. Gọi M, N là hai điểm di động trên nửa đường (O) sao cho M thuộc cung AN và tổng khoảng cách từ A, B đến MN bằng Rsqrt{3}. Gọi I là giao điểm của các đường thẳng AN và BM; K là giao điểm của AM và BN.a) Chứng minh K, M, I, N cùng thuộc một đường tròn (C).b) Tính độ dài MN và bán kính đường (C) theo Rc) Xác định vị trí M, N sao cho tam giác KAB có diện tích lớn nhất. Tính giá trị lớn nhất đó theo R.
Đọc tiếp
Cho nửa đường tròn (O) có tâm O và đường kính AB=2R. Gọi M, N là hai điểm di động trên nửa đường (O) sao cho M thuộc cung AN và tổng khoảng cách từ A, B đến MN bằng \(R\sqrt{3}\). Gọi I là giao điểm của các đường thẳng AN và BM; K là giao điểm của AM và BN.
a) Chứng minh K, M, I, N cùng thuộc một đường tròn (C).
b) Tính độ dài MN và bán kính đường (C) theo R
c) Xác định vị trí M, N sao cho tam giác KAB có diện tích lớn nhất. Tính giá trị lớn nhất đó theo R.
Cho mặt cầu (S) bán kính
R
5
c
m
. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S)(D không thuộc đường tròn (C) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
10
3
c
m
3
B.
15...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5 c m . Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S)(D không thuộc đường tròn (C) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 10 3 c m 3
B. 15 3 c m 3
C. 32 3 c m 3
D. 40 3 c m 3
Chọn C.
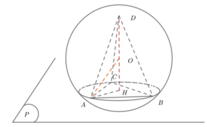
Phương pháp: Tìm vị trí điểm D để thể tích ABCD lớn nhất.
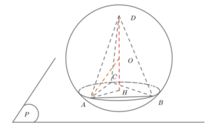
Đúng 0
Bình luận (0)
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
![]()
![]()
![]()
![]()
Cho mặt cầu (S) bán kính
R
5
c
m
. Mặt phẳng
P
cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
cm
. Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5 c m . Mặt phẳng P cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π cm . Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho mặt cầu
S
có bán kính
R
5
c
m
. Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
C
có chu vi bằng
8
π
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn
C
, điểm D thuộc
S
(D không thuộc đường tròn
C
) và tam giác ABC là...
Đọc tiếp
Cho mặt cầu S có bán kính R = 5 c m . Mặt phẳng P cắt mặt cầu S theo giao tuyến là đường tròn C có chu vi bằng 8 π . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn C , điểm D thuộc S (D không thuộc đường tròn C ) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3











