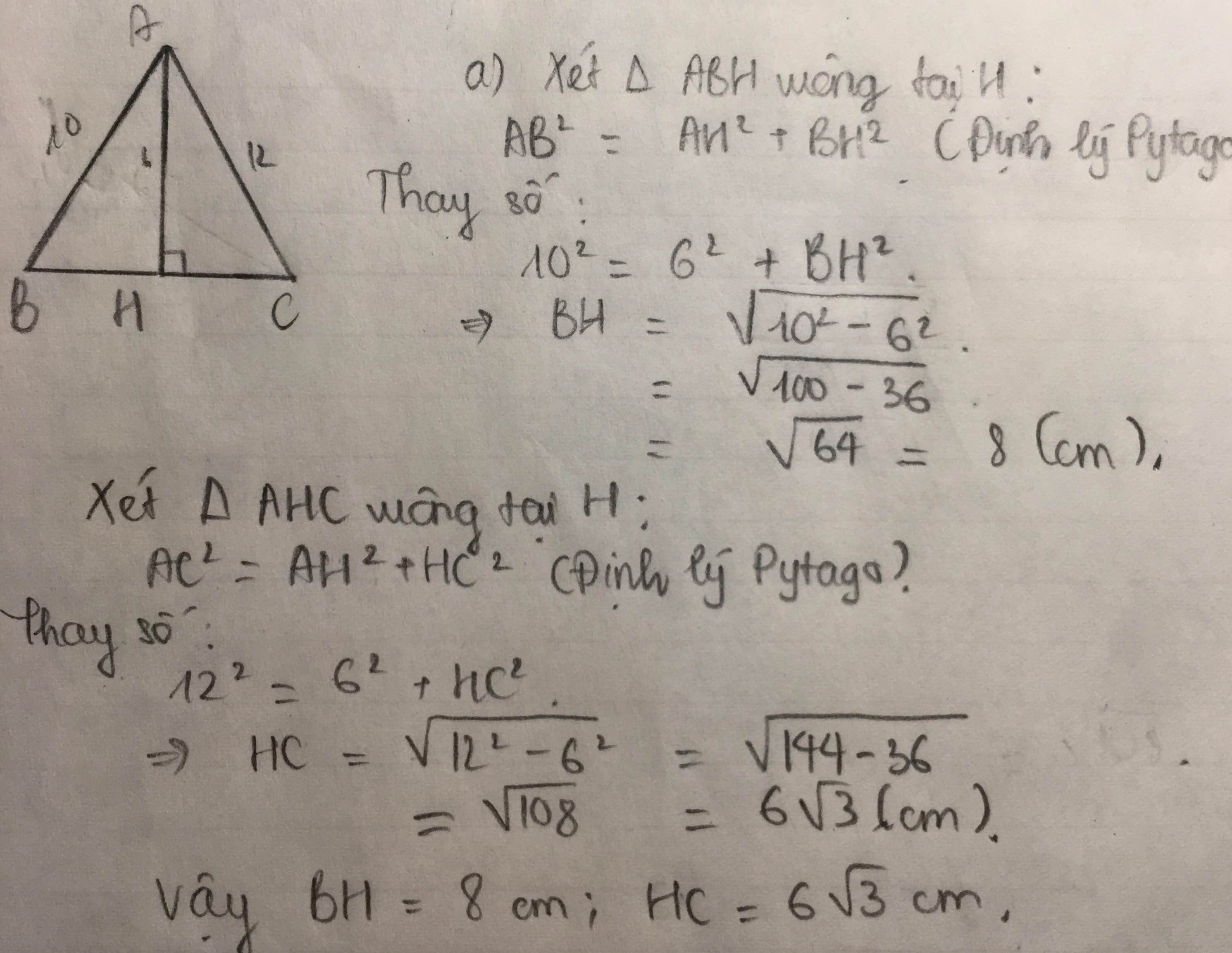Lời giải:

Áp dụng công thức hệ thức lượng trong tam giác vuông ta có:

$AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{12}=3$ (cm) 

$CH=BC-BH=12-3=9$ (cm)

Đáp án là C

Áp dụng hệ thức lượng trong tam giác vuông:

A B 2  = BH.BC = 4.(4 + 16) = 80 ⇒ AB = 4 5 cm

1: \(BC=\sqrt{12^2+9^2}=15\left(cm\right)\)

\(AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\)

\(BH=\dfrac{AB^2}{BC}=\dfrac{144}{15}=9,6\left(cm\right)\)

CH=5,4(cm)

2: \(BC=\sqrt{2+2}=2\left(cm\right)\)

\(AH=\dfrac{AB\cdot AC}{BC}=1\left(cm\right)\)

\(BH=CH=AH=1\left(cm\right)\)

Bài 1: 

AH=12cm

AC=20cm

\(\widehat{ABC}=37^0\)

Áp dụng hệ thức lượng ta có: \(AB^2=BH.BC;\) \(AC^2=HC.BC\)

=>\(\left(\frac{AB}{AC}\right)^2=\frac{BH.BC}{CH.BC}=\frac{BH}{HC}\); TA LẠI CÓ: \(\frac{AB}{AC}=\frac{3}{7}\Leftrightarrow\left(\frac{AB}{AC}\right)^2=\frac{9}{49}\Leftrightarrow\frac{BH}{CH}=\frac{9}{49}\Rightarrow BH=\frac{9}{49}.CH\)

VẪN DÙNG HỆ THỨC LƯỢNG TA CÓ: 

\(AH^2=HB.HC\Leftrightarrow HB.HC=42^2=1764\Leftrightarrow\frac{9}{49}CH.CH=1764\Leftrightarrow CH=98\Leftrightarrow BH=18\)

<br class="Apple-interchange-newline"><div id="inner-editor"></div>AB2=BH.BC; AC2=HC.BC

=>(ABAC )2=BH.BCCH.BC =BHHC ; TA LẠI CÓ: 

1: \(AC=\sqrt{25^2-20^2}=15\left(cm\right)\)

\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)

\(BH=\sqrt{20^2-12^2}=16\left(cm\right)\)

CH=BC-BC=9(cm)

2: \(BC=10cm\)

\(AC=5\sqrt{3}\left(cm\right)\)

\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)

\(BH=\dfrac{AB^2}{BC}=\dfrac{5^2}{10}=2.5\left(cm\right)\)

CH=BC-BH=7,5(cm)

Áp dụng định lí Pytago vào ΔACB vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=64-36=28\)

hay \(AC=2\sqrt{7}\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{6^2}{8}=\dfrac{36}{8}=4.5\left(cm\right)\\CH=\dfrac{28}{8}=3.5\left(cm\right)\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+HB^2\)

\(\Leftrightarrow AH^2=AB^2-BH^2=6^2-4.5^2=15.75\left(cm\right)\)

hay \(AH=\dfrac{3\sqrt{7}}{2}\left(cm\right)\)

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H co

góc B chung

=>ΔABC đồng dạng với ΔHBA

=>BA/BH=BC/BA

=>BA^2=BH*BC

b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

AH=3*4/5=2,4cm