Cho tam giác ABC có góc A = góc B. Trên các cạnh CB, CA lần lượt lấy các điểm D, E sao cho CD = CE. Gọi F là giao điểm của AD và BE. Chứng minh FA = FB".

Những câu hỏi liên quan
Cho tam giác ABC có BC là cạnh lớn nhất. Gọi I là giao điểm các đường phân giác của góc B và góc C. Trên cạnh BC lần lượt lấy các điểm D, E sao cho CD CA, BE BA.a) Chứng minh
B
I
⊥
A
E
;
C
I
⊥
A
D
.
b) Gọi M là giao điểm của BI và AD, N là giao điểm của CI và AE. Chứng minh
A
I
⊥
M
N
.
Đọc tiếp
Cho tam giác ABC có BC là cạnh lớn nhất. Gọi I là giao điểm các đường phân giác của góc B và góc C. Trên cạnh BC lần lượt lấy các điểm D, E sao cho CD = CA, BE = BA.
a) Chứng minh B I ⊥ A E ; C I ⊥ A D .
b) Gọi M là giao điểm của BI và AD, N là giao điểm của CI và AE. Chứng minh A I ⊥ M N .
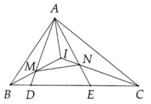
a) Tam giác ABE cân tại B có BI là phân giác nên cũng là đường cao, từ đó B I ⊥ A E . Tương tự C I ⊥ A D .
b) Từ kết quả ý a, chứng minh được I là trực tâm tam giác AMN, từ đó A I ⊥ M N
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có độ dài cạnh bằng a.Trên các cạnh AB và BC lần lượt lấy D và E sao cho AD=BE.Gọi F là giao điểm của AE và CD
a)TÍnh góc AFC
b)C/m tổng FA+FB+FC<2A
Bài 5: Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BA lấy điểm D sao cho DB BC. Tính số đo các góc của tam giác ACDBài6:TamgiácABCcântạiBcóBˆ 100 đôn.LấycácđiểmDvàEtrêncạnhAC sao cho AD BA, CE CB. Tính số đo góc DBE?Bài 7: Cho tam giác ABC cân tại A. Vẽ BH vuông góc với AC tại H. Chứng minh rằng góc BAC có số đo gấp đôi số đo góc CBH.Bài 8: Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD CE. Gọi I là giao điểm của BE và...
Đọc tiếp
Bài 5: Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BA lấy điểm D sao cho DB = BC. Tính số đo các góc của tam giác ACD
Bài6:TamgiácABCcântạiBcóBˆ =100 đôn.LấycácđiểmDvàEtrêncạnhAC sao cho AD = BA, CE = CB. Tính số đo góc DBE?
Bài 7: Cho tam giác ABC cân tại A. Vẽ BH vuông góc với AC tại H. Chứng minh rằng góc BAC có số đo gấp đôi số đo góc CBH.
Bài 8: Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD.
a) Chứng minh tam giác IBC và tam giác IDE là các tam giác cân.
b) Chứng minh BC // DE.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi
bài này dễ sao không biết
Bài 8 :
Tự vẽ hình nhé ?
a) Vì ∆ABC cân tại A (GT)
=> ∠ABC = ∠ACB (ĐN)
Mà ∠ABC + ∠DBC = 180o (2 góc kề bù)
∠ACB + ∠ECB = 180o (2 góc kề bù)
=> ∠DBC = ∠ECB (1)
Xét ∆BCD và ∆CBE có :
BD = CE (GT)
∠DBC = ∠ECB (Theo (1))
BC chung
=> ∆BCD = ∆CBE (c.g.c) (2)
=> ∠BCD = ∠CBE (2 góc tương ứng)
Hay ∠BCI = ∠CBI
Xét ∆IBC có : ∠BCI = ∠CBI (cmt)
=> ∆IBC cân tại I (định lý)
=> IB = IC (ĐN) (3)
Từ (2) => DC = EB (2 cạnh tương ứng)
Mà ID + IC = DC, IE + IB = EB
=> ID = IE
Xét ∆IDE có : ID = IE (cmt)
=> ∆IDE cân tại I (ĐN)
b) Ta có : AB + BD = AD
Mà AC + CE = AE
AB = AC (GT)
BD = CE (GT)
=> AD = AE
Xét ∆ADE có : AD = AE (cmt)
=> ∆ADE cân tại A (ĐN)
=> ∠ADE = \(\frac{180^o-\widehat{DAE}}{2}\)(4)
Vì ∆ABC cân tại A (GT)
=> ∠ABC = \(\frac{180^o-\widehat{BAC}}{2}\)(5)
Từ (4), (5) => ∠ADE = ∠ABC, mà 2 góc này ở vị trí đồng vị
=> BC // DE (DHNB)
c) Xét ∆ABM và ∆ACM có :
AM chung
AB = AC (GT)
MB = MC (do M là trung điểm của BC)
=> ∆ABM = ∆ACM (c.c.c)
=> ∠AMB = ∠AMC (2 góc tương ứng)
Mà ∠AMB + ∠AMC = 180o (2 góc kề bù)
=> ∠AMB = ∠AMC = 180o : 2 = 90o
Sau đó chứng minh ∆BIM = ∆CIM theo c.c.c bằng 3 yếu tố MI chung, MB = MC, IB = IC (Theo (3))
Rồi => ∠IMB = ∠IMC (tương ứng)
Mà ∠IMB + ∠IMC = 180o (kề bù)
=> ..... (làm như phần trên)
Ta có : ∠AMB + ∠IMB = ∠AMI
Mà ∠AMB = 90o (cmt)
∠IMB = 90o (cmt)
=> 90o + 90o = ∠AMI
=> ∠AMI = 180o
=> A, M, I thẳng hàng (đpcm)
Vậy .....
Xem thêm câu trả lời
Bài 1: Cho tam giác ABC, trên cạnh AB lấy 2 điểm D và F sao cho AD DF FB. Các trung tuyến AE, BG của tam giác ABC lần lượt cắt CD, CF tại H và K.a) CMR: GH, EK, AB cắt nhau tại 1 điểmb) CMR: AB 4HKBài 2: Cho tam giác ABC có BD và CE là phân giác, cắt nhau tại I. Gọi S là trung điểm BC, biết BI 2IS.a) CMR: tam giác ABC vuôngb) CMR: ID / IB CD / CBBài 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD AE. Qua A và D, kẻ các đường thẳng vuông góc v...
Đọc tiếp
Bài 1: Cho tam giác ABC, trên cạnh AB lấy 2 điểm D và F sao cho AD = DF = FB. Các trung tuyến AE, BG của tam giác ABC lần lượt cắt CD, CF tại H và K.
a) CMR: GH, EK, AB cắt nhau tại 1 điểm
b) CMR: AB = 4HK
Bài 2: Cho tam giác ABC có BD và CE là phân giác, cắt nhau tại I. Gọi S là trung điểm BC, biết BI = 2IS.
a) CMR: tam giác ABC vuông
b) CMR: ID / IB = CD / CB
Bài 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD = AE. Qua A và D, kẻ các đường thẳng vuông góc với BE cắt BC thứ tự tại S và T. CMR: S là trung điểm của TC
Cho tam giác ABC đều. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CB lấy điểm E, trên tia đối của tia AC lấy điểm F sao cho BD=CE=AF
a. Chứng minh tam giác DEF đều
b. Gọi P,Q,R lần lượt là giao điểm của các đường thẳng AE, DC,BF và EA,CD,FB. Chứng minh tam giác PQR là tam giác đều
Bài 2. Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho AD = AE. a) Chứng minh rằng: BE = CD b) Chứng minh rằng: góc ABE bằng góc ACD c) Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao? d) Gọi I là trung điểm BC. Chứng minh A, K, I thẳng hàng
a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Gọi M là giao điểm của BE và CD. Chứng minh:a) BE CD;b)
∆
B
M
D
∆
C
M
E
;
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh MN // AC //BD.
Đọc tiếp
Cho tam giác ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD;
b) ∆ B M D = ∆ C M E ;
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh MN // AC //BD.
Cho tam giác ABC vuông tại A, có AB= 9cm, BC= 15cm. a) Tính độ dài cạnh AC và so sánh các góc của tam giác ABC. b) Trên tia đối cua tia AB lấy điểm D sao cho AB=AD. CMR : BC=DC c) Gọi E,F lần lượt là trung điểm cạnh CD,BC; gọi I là giao điểm của BE và AC. Chứng minh D,I,F thẳng hàng.
a: AC=12cm
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
Suy ra: CB=CD
Đúng 0
Bình luận (0)
BÀI 1: Cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:a) ∆ABE ∆ADC b) Góc BMC 120oBài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).a) Chứng minh: EM + HC NH.b) Chứng minh: EN // FM.Bài 3:Cho cạnh hình vuông ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi...
Đọc tiếp
BÀI 1: Cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:
a) ∆ABE = ∆ADC b) Góc BMC = 120o
Bài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).
a) Chứng minh: EM + HC = NH.
b) Chứng minh: EN // FM.
Bài 3:Cho cạnh hình vuông ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi DAPQ bằng 2.
Chứng minh rằng : Góc PCQ = 45o
Bài 4:Cho tam giác vuông cân ABC (AB = AC), tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D.
a) Chứng minh rằng: BE = CD; AD = AE.
b) Gọi I là giao điểm của BE và CD. AI cắt BC ở M, chứng minh rằng các ∆MAB; MAC là tam giác vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE, các đường thẳng này cắt BC lần lượt ở K và H. Chứng minh rằng KH = KC.
Bài 5: Cho tam giác cân ABC (AB = AC ). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường thẳng BC cắt MN tại trung điểm I của MN.
c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.

















