cho tam giác ABC cân tại A.trên tia đối của các tia BC vad CB lấy thứ tự điểm D và E sao cho BD=CE

Những câu hỏi liên quan
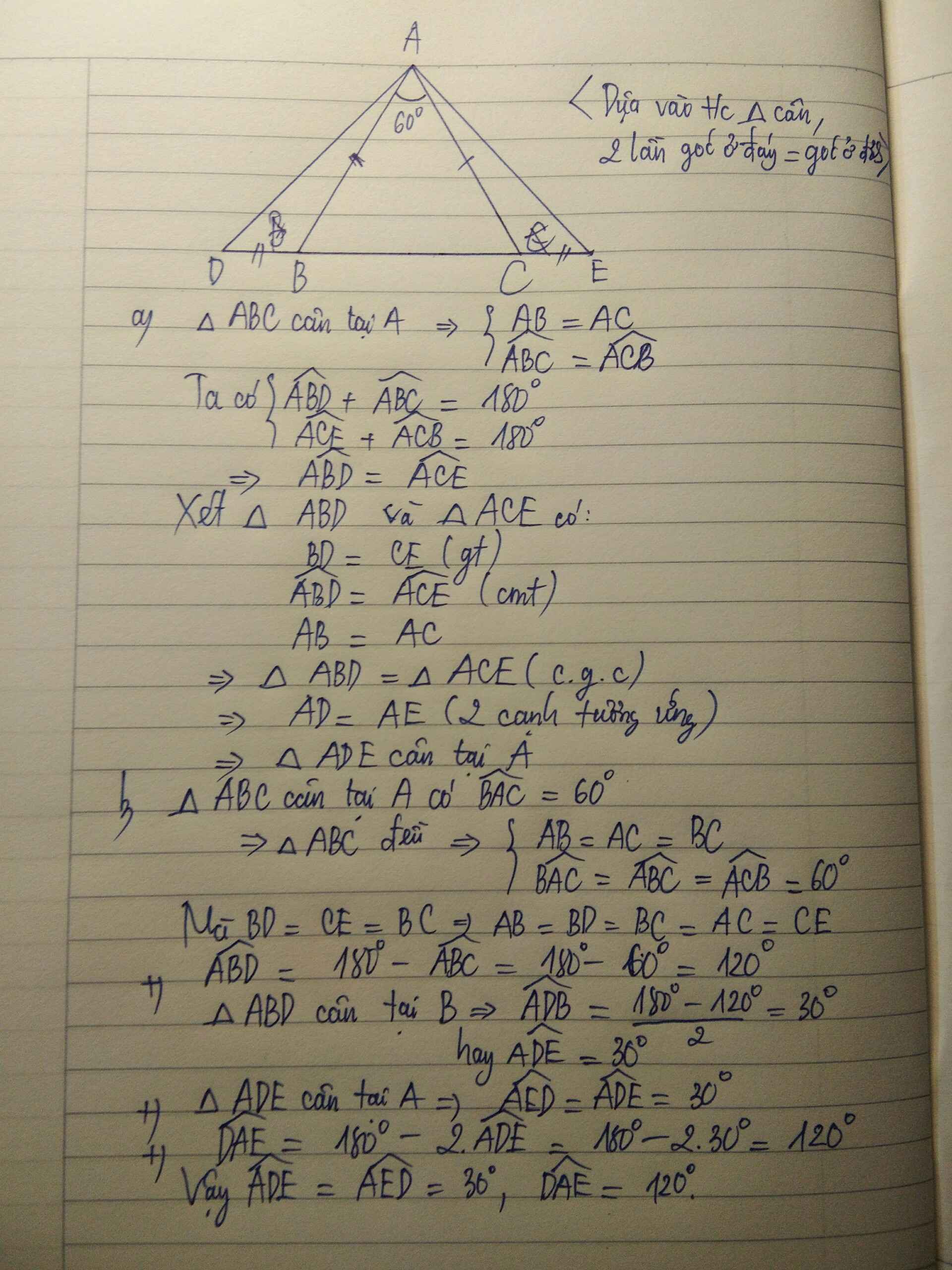
cho tam giác ABC cân tại A.trên tia đối của các tia BC vad CB lấy thứ tự hai điểm D và E sao cho BD=CE
a) chứng minh tam giác ADE cân
b) gọi M là trung điểm của BC. chứng minh AM là tia phân giác của ADE
c)từ B và C kẻ BH,CK theo thứ tự vuông góc với AD và AE (H thuộc AD,K thuộc AE).chứng minh BH=CK
d) chứng minh ba đường thẳng AM,BH,CK gặp nhau tại một điểm
a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔBAC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(Hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A.Trên tia đối của tia BC lấy điểm D sao cho AB=BD.Trên tia đối của tia CB lấy điểm E sao cho AC=CE
a)chứng minh tam giác ABC cân tại và DE=AB+AC+BC
b)tính các góc của tam giác ADE biết góc BAC=32 độ
Cho tam giác ABC cân tại A .Trên tia đối của các tia BC và CB thứ tự lấy các điểm D và E sao cho BD=CE 1) Chứng minh tam giác ADE là tam giác cân 2)Gọi M là trung điểm của BC . Chứng minh AM là tia phân giác của góc DAE 3) Từ B và C kẻ BH và CK thứ tự vuông góc với AD và AE. Chứng minh BH=CK cùng đi qua một điểm
A, xét tam giác ABD và tam giác ACE có
AB = AC ( tam giác ABC cân tại A)
MK Góc ABD + ABC = 180 độ
lại có góc ACE + ACB = 180 độ
mà góc ABC = ACB(tam giác ABC cân tại A)
=> Góc ABD =ACE
BD = CE ( GT )
nên tam giác ABD = tam giác ACE (C-G-C)
=> góc ADB = góc AEC
=> tam giác AED cân tại A
b,xét tam giác DAM và tam giác EAM có
AD = AE ( cm a, )
AM cạnh cung
mk có MB=MC(M TĐ BC) (1)
ta lại có BD = CE ( GT) (2)
từ (1) và (2) ta có
DB+BM =CE + MC
hay DM = ME
nên tam giác DAM = tam giác EAM ( C-C-C )
=> góc MAD = MAE
=>AM ph/G góc DAE
c, xét tam giác BAH và tam giác CAK có
góc BHA=CKA ( = 1 vuông )
AC =AB ( tam giác ABC cân tại A)
góc BAH = CAK ( tam giác ABD = tam giác ACE)
nên tam giác BAH = tam giác CAK ( cạnh huyền góc nhọn )
=> BH = CK
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A.Trên tia đối của tia BC lấy D,trên tia đối của tia CB lấy E sao cho BD=CE.CMR ADE là tam giác cân
cho tam giác ABC cân tại A.Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD=CE. Kẻ BH vuông góc với AD , kẻ CK vuông góc với AE . Chứng minh rằng :
a) BH=CK
b)tam giác ABH=tam giác ACK
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh:
a) tam giác ADE cân
b)Nếu cho thêm Bac = 60 độ và BD = CE = BC . Tính các góc của tam giác ADE
giúp mình với mình đang gấp !!!!
a: Xét ΔADB và ΔAEC có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hay ΔADE cân tại A
Đúng 0
Bình luận (0)
a)
Chứng minh được tam giác ABD = tam giác ACE (c-g-c) => AD = AE
Từ đó tam giác ADE cân tại A.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE, Chứng minh tam giác ADE cân.
Chứng minh được tam giác ABD = tam giác ACE (c-g-c) => AD = AE
Từ đó tam giác ADE cân tại A.
Đúng 0
Bình luận (0)
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A.Trên tia đối của tia BC và CB lấy theo thứ tự điểm D và E sao cho BD = CE
a) CMR:tam giác ADE cân
b) Gọi M là trung điểm của BC. CMR: AM là tia phân giác của góc DAE và AM vuông góc với DE
c)Từ B và C kẻ BH,CK theo thứ tự vuông góc với AD và AE .CMR: BH=CK
d)CMR:HK//BC
e) Cho HB cắt CK ở N.CMR: A,M,N thẳng hàng
toán lớp 1 mà kinh z ? bọn trẻ lớn nhanh ghê !
e chịu khó gõ link này lên google nhé!
https://h.vn/hoi-dap/question/170176.html
cái này là lớp 6 SURI chỉ chọn lớp 1 cho vui thôi
a) \(\Delta\)ABC cân ở A nên \(\widehat{ABC}=\widehat{ACB}\)mà \(\widehat{ABC}=\widehat{ABD}=90^0,\widehat{ACB}=\widehat{ACE}=90^0\)
=> \(\widehat{ABD}=\widehat{ACE}\)
AB = AC(hai cạnh bên của tam giác cân ABC)
BD = CE(gt)
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> \(\widehat{ADB}=\widehat{AEC}\)
=> AD = AE
=> \(\Delta\)ADE cân ở A
b) Ta có BD = CE(gt)
BM = CM(vì M là trung điểm của BC)
=> BD + BM = CE + CM
=> DM = EM
Xét \(\Delta ADM\)và \(\Delta AEM\)có :
AD = AE(cmt)
DM = EM(cmt)
AM chung
=> \(\Delta\)ADM = \(\Delta\)AEM(c.c.c)
=> \(\widehat{DAM}=\widehat{EAM}\)(hai góc tương ứng)
=> AM là tia phân giác của góc DAE
Ta lại có : \(\Delta\)ADM = \(\Delta\)AEM(c.c.c) => \(\widehat{DAM}=\widehat{EAM}\)(cmt)
=> \(\widehat{DAM}+\widehat{EAM}=180^0\)
=> \(\widehat{DAM}=\widehat{EAM}=90^0\)
hay \(AM\perp DE\)
c) \(\Delta\)BHD và \(\Delta\)CKE có :
BD = CE (gt)
\(\widehat{HDB}=\widehat{KEC}\)(chứng minh trên)
=> \(\Delta\)BHD = \(\Delta\)CKE (ch - gn)
=> BH = CK
d) Xét \(\Delta\)AHB và \(\Delta\)AKC có :
AB = AC(gt)
BH = CK(cmt)
=> \(\Delta\)AHB = \(\Delta\)AHC(ch - cgv)
=> AH = AK
Vì AH = AK nên \(\Delta\)AHK cân ở A,do đó \(\widehat{AHK}=\frac{180^0-\widehat{A}}{2}\)(1)
Vì AD = AE nên \(\Delta\)ADE cân ở A,do đó \(\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AHK}=\widehat{ADE}\)
Mà hai góc này ở vị trí đồng vị của hai đường thẳng DE và HK cắt đường thẳng AD,do đó HK //DE hay HK //BC
e) Xét \(\Delta\)AHN và \(\Delta\)AKN có :
AH = AK(gt)
AN chung
=> \(\Delta\)AHN = \(\Delta\)AKN(ch-cgv)
=> \(\widehat{HAN}=\widehat{KAN}\)
=> AN là phân giác \(\widehat{DAN}\)
Mà AM,AN đều là phân giác của \(\widehat{DAN}\)=> A,M,N thẳng hàng
Xem thêm câu trả lời
Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD CE. Gọi M là trung điểm của BC.a) Chứng minh rằng tam giác ADE là tam giác cân.b) Chứng minh AM là tia phân giác của góc DAE.c) Kẻ BH ⊥ AD và CK ⊥ AE. Chứng minh BH CK.d) Chứng minh ba đường thẳng AM, BH và CK đồng quy
Đọc tiếp
Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. Gọi M là trung điểm của BC.
a) Chứng minh rằng tam giác ADE là tam giác cân.
b) Chứng minh AM là tia phân giác của góc DAE.
c) Kẻ BH ⊥ AD và CK ⊥ AE. Chứng minh BH = CK.
d) Chứng minh ba đường thẳng AM, BH và CK đồng quy
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM vuông góc DE
nên AM là phân giác của góc DAE
c: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
=>BH=KC
Đúng 0
Bình luận (0)