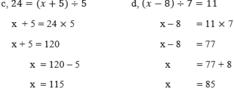Tìm X (X.7+15).23=391

Những câu hỏi liên quan
Tìm x, biết:a)
230
+
2
4
+
(
x
-
5
)
315
.
2018
0
;
b)
707
:
2
x...
Đọc tiếp
Tìm x, biết:
a) 230 + 2 4 + ( x - 5 ) = 315 . 2018 0 ;
b) 707 : 2 x - 5 + 74 = 4 2 - 3 2 ;
c) [(6x - 12): 3].32 = 64;
d) (x:7 + 15).23 = 391
bài 1 tìm x
a, 230 + [ 24 + ( x - 5 ) ] = 315 . 20200
b, 707 : [ ( 2x - 5 ) + 74 ] = 42 - 32
c, [ ( 6x - 12 ) : 3 ] . 32 = 64
d , ( x : 7 + 15 ) . 23 + 391
e , ( 19 . x + 2 . 52 ) : 14 = ( 13 - 8 ) 2 - 42
d , ( x : 7 + 15 ) . 23 + 391 => Đề thiếu
e , ( 19 . x + 2 . 52 ) : 14 = ( 13 - 8 ) 2 - 42
=> ( 19 . x + 2 . 52 ) : 14 = 52 - 16
=> ( 19 . x + 2 . 52 ) : 14 = 25 - 16 = 9
=> 19 . x + 2 . 52 = 9 x 14 = 126
=> 19 . x + 2 . 25 = 126
=> 19 . x + 50 = 126
=> 19 . x = 126 - 50 = 76
=> x = 76 : 19 = 4
a, 230 + [ 24 + ( x - 5 ) ] = 315 . 20200
=> 230 + [16 + ( x - 5 ) ] = 315 . 1
=> 230 + [ ( 16 - 5 ) + x ) = 315
=> 11 + x = 315 - 230 = 85
=> x = 85 - 11 = 74
b, 707 : [ ( 2x - 5 ) + 74 ] = 42 - 32
=> 707 : [ ( 2x - 5 ) + 74 ] = 16 - 9 = 7
=> ( 2x - 5 ) + 74 = 707 : 7 = 101
=> 2x - 5 = 101 - 74 = 27
=> 2x = 27 + 5 = 32
=> 2x = 25
=> x = 5
Xem thêm câu trả lời
Tìm số tụ nhiên x biết:
a. (x – 45).27 = 0 b. 23.(42- x) = 23
c. 3x – 5=7 e. 15 – 5x=10
Xem chi tiết
a) (x – 45).27 = 0
=> x - 45 = 0
=> x = 45
b) 23.(42- x) = 23
=> 42- x = 1
=> x = 41
c. 3x – 5=7
=> 3x = 12
=> x = 4
e. 15 – 5x=10
=> 5x = 5
=> x = 1
Tìm x biết:
a, (x + 15)÷8 = 7
b, (x - 23)÷8 = 12
c, 24 = (x + 5)÷5
d, (x - 8)÷7 = 11
Tìm x biết
13-x+14-23=-7+3-15
Tìm x € Z
Câu 8:
5-|x-4|=-7+(23-54)-(-54+23)
Câu 9:
|x+7|=15+|-27|-(13-17+|-20|)
Câu 10:
|x-7|+24=24-x+(-24)+x+|-40|
Bài 1: Tìm x, biết:
a) -15 + (53 – x) = 13 – (4 – 10)
b) 11 – (25 – x + 11) = - (45 – 7)
c) 23 + (63 – 7) = 5 – (23 - x)
d) 114 – (72 – x) = 24 – (25 – 43)
Tìm số nguyên x, biết: a) (-15).x = 10.(- 4) - 5; b) (- 3).x - 4 = 2. (- 7) + 4 c) 7.x + l = -13; a) (- 8).x + 17 = - 23;
Tìm x : -15/23 : 22x/7=-14x/11: 13 4/5
\(-\dfrac{15}{23}:\dfrac{22x}{7}=-\dfrac{14x}{11}:\left(13+\dfrac{4}{5}\right)\)
=>\(-\dfrac{15}{23}\cdot\dfrac{7}{22x}=\dfrac{-14x}{11}:\dfrac{69}{5}\)
=>\(-\dfrac{105}{23\cdot22x}=\dfrac{-70x}{11\cdot69}\)
=>\(\dfrac{-3}{2x}=\dfrac{-2x}{3}\)
=>\(4x^2=9\)
=>\(x^2=\dfrac{9}{4}\)
=>\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)