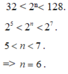Tìm N thuộc n biết 8 ≤ 2n ≤ 128

Những câu hỏi liên quan
Tìm N thuộc n biết 8 ≤ 2n ≤ 128
Lời giải:
$8\leq 2n\leq 128$
$\Rightarrow \frac{8}{2}\leq n\leq \frac{128}{2}$
$\Rightarrow 4\leq n\leq 64$
$\Rightarrow n\in\left\{4; 5; 6; ....; 63; 64\right\}$
Đúng 1
Bình luận (0)
1.Tìm n thuộc N* biết 2n+1 và 3n+1 là số chính phương.
2.Tìm m,n thuộc N* biết 3m=n2+2n-8
TÌM n thuộc N biết(2n+8) chia hết cho (2n+1)
Theo bài ra ta có:
2n + 8 chia hết cho 2n + 1
=> ( 2n + 1 ) + 7 chia hết cho 2n + 1
=> 7 chia hết cho 2n + 1
=> 2n + 1 thuộc { 1 ; 7 }
=> 2n thuộc { 0 ; 6 }
=> n thuộc { 0 ; 3 }
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết: 32 < 2n< 128
Tìm x thuộc N biết: \(8^x< 128^3\)
tìm n thuộc N, biết 8 chia hết cho (2n-1)
Ta có: \(8⋮\left(2n-1\right)\Rightarrow2n-1\inƯ\left(8\right)\)
Mà \(n\in N\Rightarrow2n-1=1\)
\(\Rightarrow2n=2\Rightarrow n=1\)
Vậy n = 1
Đúng 0
Bình luận (0)
tìm n thuộc N biết 3n+8 chia hết cho 2n+3
Tìm n thuộc N sao,,biết 2+4+6+8+......{2n}=756
Ta có 2 + 4 + 6 + 8 + ... + 2n = 756
=> 2(1 + 2 + 3 + 4 + ... + n) = 756
=> 2.n(n + 1) : 2 = 756
=> n(n + 1) = 756
=> n2 + n - 756 = 0
=> n2 - 27n + 28n - 756 = 0
=> n(n - 27) + 28(n - 27) = 0
=> (n + 28)(n - 27) = 0
=> \(\orbr{\begin{cases}n=-28\left(\text{loại}\right)\\n=27\left(tm\right)\end{cases}}\)
Vậy n = 27
viết các số sau về dạng lũy thừa của 1 số tự nhiên:125;27;64;1296;1024;2401;43;8;25.125
tìm n là số tự nhiên,biết
2n16 3n81 2n-164 3n+227.81 25.5n-1625
2n.8128 3.5n375 (3n)2729 81≤3n≤729 (2n-1)481
(n-2)3125 (n-1)532.243
bài khó quá ,giúp mình với
Đọc tiếp
viết các số sau về dạng lũy thừa của 1 số tự nhiên:125;27;64;1296;1024;2401;43;8;25.125
tìm n là số tự nhiên,biết
2n=16 3n=81 2n-1=64 3n+2=27.81 25.5n-1=625
2n.8=128 3.5n=375 (3n)2=729 81≤3n≤729 (2n-1)4=81
(n-2)3=125 (n-1)5=32.243
bài khó quá ,giúp mình với
1. (Mình đưa nó về thừa số nguyên tố nha, cái nào ko đc thì thôi)
125 = 53; 27 = 33; 64 = 26; 1296 = 64; 1024 = 210; 2401 = 74; 43 = 64; 8 = 23; 25.125 = 3125 = 55.
2.
2n = 16 =) n = 4. 3n = 81 =) n = 4. 2n-1 = 64 =) n = 7. 3n+2 = 27.81 =) n = 5. 25.5n-1 = 625 =) n = 3.
2n.8 = 128 =) n = 4. 3.5n = 375 =) n = 3. (3n)2 = 729 =) n = 3. 81 ≤ 3n ≤ 729 =) n = 4; 5; 6.
Đúng 0
Bình luận (0)
\(125=5^3;27=3^3;1296=36^2=6^4=2^4.3^4;1024=32^2=2^{10};2401=49^2=7^4;4^3=2^6;8=2^3;25.125=5^2.5^3=5^5\)
Đúng 0
Bình luận (0)