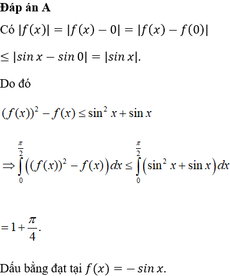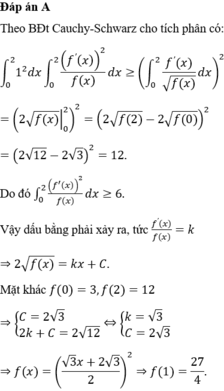Cho hàm số \(f(x)\) thoả mãn \(f(1) = 2\) và \(f'(x) = {x^2}f(x)\) với mọi \(x\). Tính \(f''(1)\).

Những câu hỏi liên quan
cho hàm số f(x) xác định với mọi x thoả mãn f(x1.x2)=f(x1).f(x2) và f(2)=0,75 tính f(8)
Cho hàm số y=f(x) thoả mãn f(x)+xf(x/2x-1)=2 mọi x\{1;1/2}. Tính f(5)
cho hàm số f(x) xác định với mọi x thoả mãn f(x1.x2)=f(x1).f(x2) và f(2)=0,75 tính f(8)
Cho hàm số y=f(x) thoả mãn f(2x+1)=(x-12)(x+13) với mọi x. Tính f(31)
f(x)=f(2x+1)=(x-12)(x+13)=f(31) =>2x+1=31 =>x=15
=>f(31)=(x-12)(x+13)=(15-12)(15+13)=84
Đúng 0
Bình luận (0)
Cho hàm số yf(x) thoả mãn f(-2)3, f(2)2 và bảng xét dấu của đạo hàm như sau:Bất phương trình
3
f
(
x
)
+
m
≤
4
f
(
x
)
+
1
+
4
m
nghiệm đúng với mọi số thực
x
∈
-
2
;
2...
Đọc tiếp
Cho hàm số y=f(x) thoả mãn f(-2)=3, f(2)=2 và bảng xét dấu của đạo hàm như sau:
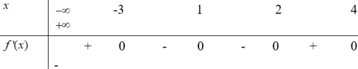
Bất phương trình 3 f ( x ) + m ≤ 4 f ( x ) + 1 + 4 m nghiệm đúng với mọi số thực x ∈ - 2 ; 2 khi và chỉ khi
A. m ∈ - 2 ; - 1
B. m ∈ - 2 ; - 1
C. m ∈ - 2 ; 3
D. m ∈ - 2 ; 3
Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
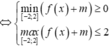
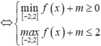
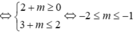
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục trên R thoả mãn f(0)0 và
|
f
(
x
)
-
f
(
y
)
|
≤
|
sin
x
-
sin
y
|
với mọi
x
,
y
∈
R
. Giá trị lớn nhất của tích phân
∫
0
π
2
(
(
f
(
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thoả mãn f(0)=0 và | f ( x ) - f ( y ) | ≤ | sin x - sin y | với mọi x , y ∈ R . Giá trị lớn nhất của tích phân ∫ 0 π 2 ( ( f ( x ) ) 2 - f ( x ) ) d x bằng
A. π 4 +1
B. π 8
C. 3 π 8
D. 1- π 4
Cho hàm số f(x) xác định với mọi x thỏa mãn f (a+b) = f (a.b) và f (-1/2) = -1/2 . Tính f ( 2016)
Với mọi x thỏa mãn: f( a + b ) = f (ab)
=>f( 0 ) = f( -1/2 . 0 ) = f ( -1/2 + 0 ) = f( -1/2 ) = -1/2
=> f ( 2006 ) = f ( 2006 + 0 ) = f(2006 . 0 ) = f(0 ) = -1/2
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0)3,f(2)12 và
∫
0
2
(
f
(
x
)
)
2
f
(
x
)
d
x
6...
Đọc tiếp
Cho hàm số f (x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0)=3,f(2)=12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 . Tính f(1).
A. 27 4
B. 25 4
C. 9 2
D. 15 4
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) 3; f(2) 12 và
∫
0
2
(
f
(
x
)
)
2
f
(
x
)
d
x...
Đọc tiếp
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) = 3; f(2) = 12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 Tính f(1)
A. 27/4
B. 25/4
C. 9/2
D. 15/4
Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
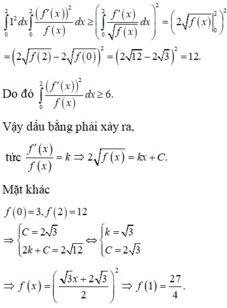
Đáp án A
Đúng 0
Bình luận (0)