Cho tam giác ABC vuông ở A có AB<AC. AH vuông góc với BC tại H, D là điểm trên cạnh BC sao cho AD=AB. Vẽ DE vuông góc với BC tại E.a\ Chứng minh rằng AH=HE.
b\Lấy I là trung điểm cua BD, tính góc AHI
Câu a\ mình làm được rồi nhé
Cho tam giác ABC vuông ở A và tam giác DEF vuông ở D có AB = DE và góc ABC = góc DEF. Chứng minh tam giác ABC = tam giác DEF.
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
cho tam giác abc vuông ở A có chu vi = 24m có cạch ab = 3/4 ac ,ab= 10m .Tính diện tích tam giác abc.
Tổng độ dài hai cạnh AB và AC là :
24 - 10 = 14 ( cm )
Độ dài cạnh AB là :
14 : ( 3 + 4 ) x 3 = 6 ( cm )
Độ dài cạnh AC là :
14 - 6 = 9 ( cm )
Diện tích hình tam giác ABC là :
6 x 9 : 2 = 27 ( cm2)
Đáp số : 27 cm2
tổng độ dài hai cạnh là
24-10=14 cm
độ dại cạnh AB là
14:(3+4).3=6 cm
độ dài cạnh AC là
14-6=8 cm
diện tích là
6.7:2=27cm2
đáp số...............

Thảo Mai bạn tham khảo đây nhé:
Câu hỏi của Tran Quynh Anh - Toán lớp 5 - Học toán với OnlineMath
......
 Thảo Mai
Thảo Mai
Cho tam giác ABC vuông ở A có A B = 10 c m , A C = 24 c m . So sánh các góc của tam giác ABC
A. A < B < C
B. A > B > C
C. B < A < C
D. C < A < B
Do tam giác ABC vuông tại A nên góc A là góc lớn nhất
Có AB < AC ⇒ C < B . Từ đó suy ra ∠C < ∠B < ∠A hay ∠A > ∠B > ∠C . Chọn B
Cho tam giác ABC vuông ở A có và AB = 6cm. Tính các cạnh của tam giác.
vì trong tam giác vuông tại A nên =>AB=AC;B=C
vì AB=AC(cmt)=>AC=6cm
còn BC thì thì tui chịu
TK:
Định lí pi-ta-go
Ta giác ABC vuông tại A=> AB và AC là cạnh góc vuông còn BC là cạnh huyền
=>AB2+AC2=BC2
hay 62+82=BC2
=>100=BC2
=>BC2=102
=>BC=10cm
Cho tam giác vuông ABC vuông ở A có chu vi 237,6cm.Cạnh AB dài hơn cạnh AC 19,8dm.Cạnh BC dài 99dm.Tính diện tích hình tam giác vuông ABC.
a:
Sửa đề tam giác DEC
Xet ΔABC vuông tại A và ΔDEC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDEC
b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)
\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)
AD là phân giác
=>BD/AB=CD/AC
=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)
=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)
cho tam giác ABC vuông ở B có AB=2, góc BAC = 30 độ. Giải tam giác vuông ABC.
Ta có:
\(\widehat{B}=180^o-90^o-30^o=60^o\)(tổng 3 góc trong tam giác)
\(AC=2BC\)(cạnh đối diện góc 30 độ)
Áp dụng định lý Pytago
\(AC^2=BC^2+AB^2\)
\(3BC^2=4\Rightarrow BC=\dfrac{2\sqrt{3}}{3}\)\(\Rightarrow AC=\dfrac{4\sqrt{3}}{3}\)
Cho tam giác vuông ABC vuông ở A có chu vi 237,6cm. Cạnh AB dài hơn cạnh AC 19,8dm. Cạnh BC dài 99dm. Tính diện tích tam giác vuông ABC
Cho tam giác vuông ABC vuông ở A có chu vi 237,6dm. Cạnh AB dài hơn cạnh AC 19,8dm. Cạnh BC dài 99dm. Tính diện tích tam giác vuông ABC.
bài giải
Tổng độ dài cạnh AB và AC là :
237,6 - 99 = 138,6 ( dm )
Độ dài cạnh AB là :
(138,6 + 19,8) : 2 = 79,2 ( dm )
Độ dài cạnh AC là :
79,2 - 19,8 = 59,4 ( dm )
Diện tích hình tam giác vuông là :
79,2 x 59,4 : 2 = 2352,24 ( dm2 )
bài giải
Tổng độ dài cạnh AB và AC là :
237,6 - 99 = 138,6 ( dm )
Độ dài cạnh AB là :
(138,6 + 19,8) : 2 = 79,2 ( dm )
Độ dài cạnh AC là :
79,2 - 19,8 = 59,4 ( dm )
Diện tích hình tam giác vuông là :
79,2 x 59,4 : 2 = 2352,24 ( dm2 )
bài giải
Tổng độ dài cạnh AB và AC là :
237,6 - 99 = 138,6 ( dm )
Độ dài cạnh AB là :
(138,6 + 19,8) : 2 = 79,2 ( dm )
Độ dài cạnh AC là :
79,2 - 19,8 = 59,4 ( dm )
Diện tích hình tam giác vuông là :
79,2 x 59,4 : 2 = 2352,24 ( dm2 )
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
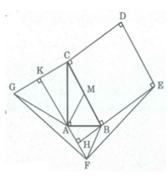
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )