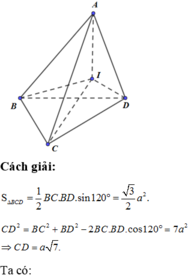
Cho tứ giác ABCD. Biết AB+BD<AC+CD. Chứng minh AB<AC

Những câu hỏi liên quan
cho tứ giác abcd có ab+dc+ac=10cm. tính đường chéo bd biết diện tích tứ giác abcd đạt gtln
Cho tứ giác ABCD có đg chéo BD chia tứ giác thành 2 tam giác đồng dạng. Tam giác ABD và Tam giác BDCa, CMR. AB//CDb, Tính BD,NC biết AB =2 cm, AD=3cm,CD=8cm.
Bài làm
a) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\widehat{ABD}=\widehat{BDC}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong
=> AB // CD
b) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\frac{AB}{CD}=\frac{AD}{BC}=\frac{BD}{BD}\)
hay \(\frac{2}{8}=\frac{3}{BC}=\frac{BD}{BD}\)
=> BC = 8 . 3 : 2 = 12 ( cm )
cho tứ giác abcd có ac vuong góc với bd. kẻ bh vuông góc với cd(h thuộc cd)
a) biết ab//cd ,bh=4cm ,bd=5cm ,tính ac ?
b) biết ab=1/2cd;ao=1/3ac diện tích tam giác aob bằng 4cm2 tính diện tích tứ giác abcd
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Tính các độ dài BD, BC biết AB = 2cm, AD = 3cm, CD = 8cm.
A. BD = 5cm, BC = 6cm
B. BD = 6cm, BC = 4cm
C. BD = 6cm, BC = 6cm
D. BD = 4cm, BC = 6cm
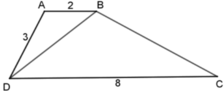
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có đg chéo BD chia tứ giác thành 2 tam giác đồng dạng. Tam giác ABD và Tam giác BDC
a, CMR. AB//CD
b, Tính BD,NC biết AB =2 cm, AD=3cm,CD=8cm.
Cho tứ diện ABCD có ABACAD2a. Biết tam giác BCD có BC2a, BDa,
C
B
D
^
120
°
. Tính thể tích tứ diện ABCD theo a
Đọc tiếp
Cho tứ diện ABCD có AB=AC=AD=2a. Biết tam giác BCD có BC=2a, BD=a, C B D ^ = 120 ° . Tính thể tích tứ diện ABCD theo a
![]()
![]()
![]()
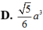
Cho tứ diện ABCD có AB AC AD 2a. Biết tam giác BCD có BC 2a, BD a,
C
B
D
^
120
0
. Tính thể tích tứ diện ABCD theo a. A.
5
3
a
3
B.
5
2
a
3...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD = 2a. Biết tam giác BCD có BC = 2a, BD = a, C B D ^ = 120 0 . Tính thể tích tứ diện ABCD theo a.
A. 5 3 a 3
B. 5 2 a 3
C. 5 a 3
D. 5 6 a 3
Phương pháp:
Sử dụng các công thức diện tích tam giác ![]() và công thức Cosin
và công thức Cosin ![]()
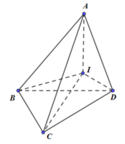
Cách giải:
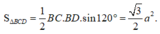
![]()
![]()
Ta có: ![]()
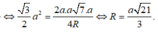
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD ![]()
![]()
Thể tích tứ diện ABCD là 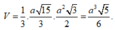
Chọn D.
Đúng 0
Bình luận (0)
Tứ giác ABCD có góc A = 90 độ . BD vuông góc với BC . Biết AB = 2cm; BD = 3cm ; DC = 4,5cm . Xét dạng của tứ giác ABCD
Cho tứ giác ABCD có AB AD, CB CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).a) Chứng minh AC là đường trung trực của BD.b) Tính
B
^
,
D
^
b
i
ế
t
A
^
100
O
,
C
^
...
Đọc tiếp
Cho tứ giác ABCD có AB = AD, CB = CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).
a) Chứng minh AC là đường trung trực của BD.
b) Tính B ^ , D ^ b i ế t A ^ = 100 O , C ^ = 60 O
a) HS tự chứng minh
b) Sử dụng tổng bốn góc trong tứ giác và chú ý B ^ = D ^
Đúng 0
Bình luận (0)