Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?
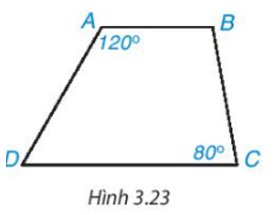
hình thang có 2 cạnh bên =nhau có phải là hình thang cân k vì sao
hình thang có 2 cạn bên bằng nhau
có 2 góc bằng nhau
thì mới suy ra là hình thang cân
Trong các hình sau, hình nào nội tiếp được trong một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
Các hình nội tiếp được trong một đường tròn là:
+ Hình chữ nhật:
Hình chữ nhật ABCD có:
⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.
+ Hình vuông:
Vì hình vuông là hình chữ nhật
⇒ Hình vuông cũng nội tiếp trong một đường tròn.
+ Hình thang cân:
Hình thang cân ABCD có:
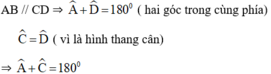
⇒ ABCD nội tiếp trong một đường tròn.
Trong các hình sau, hình nào nội tiếp được trong một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
Các hình nội tiếp được trong một đường tròn là:
+ Hình chữ nhật:
Hình chữ nhật ABCD có:
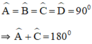
⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.
+ Hình vuông:
Vì hình vuông là hình chữ nhật
⇒ Hình vuông cũng nội tiếp trong một đường tròn.
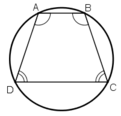
+ Hình thang cân:
Hình thang cân ABCD có:
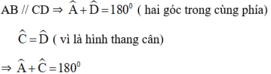
⇒ ABCD nội tiếp trong một đường tròn.
Trong các hình sau, hình nào nội tiếp được trong một đường tròn: Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng 180o.Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là 90o + 90o = 180o
Hình thang nói chung, hình thang vuông không nội tiếp được đường tròn.
Hình thang cân ABCD (BC= AD) có hai góc ở mỗi đáy bằng nhau
=
,
=
; mà
+
= 180o (hai góc trong cùng phía tạo bởi cát tuyến AD với AD // CD),suy ra
+
= 180o . Vậy hình thang cân luôn có tổng hai góc đối diện bằng 180o nên nội tiếp được đường tròn
Tại sao không thể chỉ ra hình thang có hai cạnh bên bằng nhau là hình thang cân?
vì nếu 2 cạnh ben bằng nhau và 2 cạnh đáy song song (có thể) là hình bình hành
Cho hình thang ABCD ( AB//CD). GọiM,N,P,Q lần lượt là các trung điểm của các cạnh AB,AC,CD,BD
a)Tứ giác MNPQ là hình gì ? Vì sao ?
b)Nếu tứ giác ABCD là hình thang cân thì tứ giác MNPQ là hình gì ? Vì sao ?
c)Hình thang ABCD có thêm điều kiện gì để tứ giác MNPQ là hình vuông.
Tam giác BCD có :
BN = NC ( gt )
DP = PC ( gt )
\(\Rightarrow\)NP là đường trung bình tam giác BCD ( 1 )
Tam giác ADB có :
AQ = QD ( gt )
AM = MB ( gt )
\(\Rightarrow\)QM là đường trung bình tam giác ADB ( 2 )
Từ ( 1 ) , ( 2 ) suy ra NP = QM , NP // QM
\(\Rightarrow\)MNEF là hình bình hành ( đến đây bạn tự chứng minh tiếp hình thoi )
c) Để MNPQ là hình vuông thì ta chứng minh ABCD là hình thang cân có 2 đường chéo vuông góc với nhau
Cho hình bên, trong đó ABCD là hình thang.
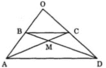
a, Trong hình thang đó những tam giác nào có diện tích bằng nhau? Vì sao?
b, Biết chiều cao của tam giác OBC kẻ từ O bằng chiều cao của hình thang ABCD. Hãy tìm trong hình thang đó xem những tam giác nào có diện tích bằng diện tích hình tam giác OBC. Vì sao?
a, Diện tích BAD = diện tích CAD (chung đáy AD, các đường cao vẽ từ B, C đến AD bằng nhau)
Diện tích ABC = diện tích BDC (chung đáy BC, các đường cao vẽ từ A và D đến BC bằng nhau)
Suy ra diện tích ABM bằng diện tích DCM
b, Diện tích ABC = diện tích DBC = diện tích OBC (chung đáy BC và 3 đường cao vẽ từ A, D, O đến BC bằng nhau)
Hình thang ABCD có AB // CD và ACD=BDC. Hình thang ABCD có phải là hình thang cân không?
Bài giải
Hình thang ABCD có \(\hept{\begin{cases}AB\text{ }//\text{ }CD\\\widehat{ACD}=\widehat{BDC}\end{cases}}\) thì hình thang ABCD là hình thang cân
Cho hình thang ABCD (AB//CD). Gọi MNPQ theo thứ tự là trung điểm của AB, AC ,CD,BD
a, chứng minh rằng MNPQ là hình bình hành
b, Nếu ABCD là hình thang cân thì tứ giác MNPQ là hình gì? VÌ sao?
c, HÌnh thang ABCD có thêm điều kiện gì thì MNPQ là hình vuông
(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi
Giải hộ mình với mai mình thi học sinh giỏi rùi!
Chứng minh rằng nếu một tứ giác có tâm đối xứng thì đó là hình bình hành. (đừng nhầm với hình thang cân nha vì hình thang cân không có tâm đối xứng đâu)