Tìm giá trị nguyên của x để biểu thức A có giá trị nguyên: A=6x^2-9x-13/3x-4

Những câu hỏi liên quan
tìm giá trị nguyên của x để biểu thức A có giá trị nguyên : A=(6x^2-9x-13)/(3x-4)
Bài 2: Cho biểu thức A=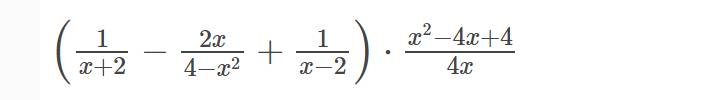
a) tìm điều kiện của A để xác định
b) Rút gọn biểu thức A
Câu 6: tìm các giá nguyên của x để để giá trị biểu thức 9x+4/3x+1 là một số nguyên
Câu 6:
ĐKXĐ: \(x\ne-\dfrac{1}{3}\)
Để \(\dfrac{9x+4}{3x+1}\in Z\) thì \(9x+4⋮3x+1\)
=>\(9x+3+1⋮3x+1\)
=>\(1⋮3x+1\)
=>\(3x+1\in\left\{1;-1\right\}\)
=>\(3x\in\left\{0;-2\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3}\right\}\)
mà x nguyên
nên x=0
Câu 2:
a: ĐKXĐ: \(x\notin\left\{2;-2;0\right\}\)
b: \(A=\left(\dfrac{1}{x+2}-\dfrac{2x}{4-x^2}+\dfrac{1}{x-2}\right)\cdot\dfrac{x^2-4x+4}{4x}\)
\(=\left(\dfrac{1}{x+2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x-2}\right)\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{x-2+2x+x+2}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{4x\left(x-2\right)}{4x\left(x+2\right)}=\dfrac{x-2}{x+2}\)
Đúng 2
Bình luận (0)
Cho biểu thức \(A=\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)
a, Tìm điều kiện của x để giá trị của phân thức xác định
b, Rút gọn biểu thức
c, Tính giá trị biểu thức khi x = 4
d, Tìm giá trị nguyên của x để A có giá trị là số nguyên.
a,ĐK: \(\hept{\begin{cases}x\ne0\\x\ne\pm3\end{cases}}\)
b, \(A=\left(\frac{9}{x\left(x-3\right)\left(x+3\right)}+\frac{1}{x+3}\right):\left(\frac{x-3}{x\left(x+3\right)}-\frac{x}{3\left(x+3\right)}\right)\)
\(=\frac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\frac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)
\(=\frac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}.\frac{3x\left(x+3\right)}{-x^2+3x-9}=\frac{-3}{x-3}\)
c, Với x = 4 thỏa mãn ĐKXĐ thì
\(A=\frac{-3}{4-3}=-3\)
d, \(A\in Z\Rightarrow-3⋮\left(x-3\right)\)
\(\Rightarrow x-3\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\Rightarrow x\in\left\{0;2;4;6\right\}\)
Mà \(x\ne0\Rightarrow x\in\left\{2;4;6\right\}\)
Đúng 1
Bình luận (0)
Cho biểu thức: \(A=\frac{3x^2-11x+6}{x^2-6x+9}\)
a, Tìm giá trị của x để A=0
b, Tìm giá trị nguyên của x để A có giá trị nguyên
ĐKXĐ : x2 - 6x + 9 \(\ne\)0
<=> x \(\ne\)3
a) A = 0
=> 3x2 - 11x + 6 = 0
<=> 3x2 - 9x - 2x + 6 = 0
<=> 3x(x - 3) - 2(x - 3) = 0
<=> (3x - 2)(x - 3) = 0
<=> \(\orbr{\begin{cases}x=\frac{2}{3}\left(tm\right)\\x=3\left(\text{loại}\right)\end{cases}}\)
Vậy x = 2/3 thì A = 0
b) Ta có A = \(\frac{3x^2-11x+6}{x^2-6x+9}=3+\frac{7x-21}{x^2-6x+9}=3+\frac{7}{x-3}\)
Để : A \(\inℤ\Leftrightarrow7⋮x-3\Leftrightarrow x-3\inƯ\left(7\right)\Leftrightarrow x-3\in\left\{1;7;-1;-7\right\}\)
Lập bảng xét các trường hợp
| x - 3 | 1 | 7 | -1 | -7 |
| x | 4(tm) | 10(tm) | 2(tm) | -4(tm) |
Vậy \(x\in\left\{4;10;2;-4\right\}\)thì A \(\inℤ\)
Cho 2 biểu thức:
A=\(\frac{4x-7}{x-2}\)
B=\(\frac{3x^2-9x+2}{x-3}\)
a,Tìm giá trị nguyên của x để mỗi biểu thức có giá trị nguyên
b,Tìm giá trị nguyên của x để cả hai biểu thức cùng có giá trị nguyên.
Giúp mik với mik đnag cần gấp ạ!!!!!!!!!!!!
Cho biểu thức: A=\(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{x^2-4}\)
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A khi x = -2 và x = 4.
c) Tìm x biết A = 3.
d) Tìm giá trị nguyên của x để biểu thức A có giá trị nguyên.
a: \(A=\dfrac{x^2-2x+2x^2+4x-3x^2-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)
Đúng 0
Bình luận (0)
a, \(\dfrac{x}{x+2}\) + \(\dfrac{2x}{x-2}\) -\(\dfrac{3x^2-4}{x^2-4}\)
= \(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{x^2-4}\)
= \(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{\left(x+2\right)\left(x-2\right)}\)
= \(\dfrac{x\left(x-2\right)+2x\left(x+2\right)-3x^2-4}{\left(x+2\right)\left(x-2\right)}\)
= \(\dfrac{2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2}{x+2}\)
Có vài bước mình làm tắc á nha :>
Đúng 0
Bình luận (0)
Cho biểu thức A=\(\frac{3x^3-14x^2+3x+36}{3x^3-19x^2+33x-9}\)
a) Tím giá trị của x để biểu thức A xác định
b)Tìm giá trị của x để biểu thức A có giá trị bằng 0
c) Tìm giá trị nguyên của x để biểu thức A có giá trị nguyên
a, A xác định
\(\Leftrightarrow3x^3-19x^2+33x-9\ne0\)
\(\Leftrightarrow3x^3-x^2-18x^2+6x+27x-9\ne0\)
\(\Leftrightarrow x^2\left(3x-1\right)-6x\left(3x-1\right)+9\left(3x-1\right)\ne0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-3\right)^2\ne0\Leftrightarrow\hept{\begin{cases}x\ne\frac{1}{3}\\x\ne3\end{cases}}\)
b, \(\frac{3x^3-14x^2+3x+36}{3x^2-19x^2+33x-9}=\frac{3x^2\left(x-3\right)-5x\left(x-3\right)-12\left(x-3\right)}{\left(3x-1\right)\left(x-3\right)^2}\)
\(=\frac{\left(3x^2-5x-12\right)\left(x-3\right)}{\left(3x-1\right)\left(x-3\right)^2}=\frac{\left(3x+4\right)\left(x-3\right)^2}{\left(3x-1\right)\left(x-3\right)^2}=\frac{3x+4}{3x-1}\)
\(A=0\Leftrightarrow\frac{3x+4}{3x-1}=0\Leftrightarrow3x+4=0\Leftrightarrow x=-\frac{4}{3}\) (thỏa mãn ĐKXĐ)
c, \(A=\frac{3x+4}{3x-1}=1+\frac{5}{3x-1}\in Z\Rightarrow5⋮\left(3x-1\right)\)
\(\Rightarrow3x-1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow x\in\left\{-\frac{4}{3};0;\frac{2}{3};2\right\}\)
Mà \(x\in Z,x\ne\left\{\frac{1}{3};3\right\}\Rightarrow x\in\left\{0;2\right\}\)
Đúng 0
Bình luận (0)
Bài của Hùng rất thông minh
Đang định có cách khác mà dài hơn cách Hùng nên thui
^^ 2k5 kết bạn nhé
Đúng 0
Bình luận (0)
Bài 1: Giải phương trình sau:2x^2+5+2sqrt{x^2+x-2}5sqrt{x-1}+5sqrt{x+2}Bài 2: Cho biểu thứcPleft(frac{6x+4}{3sqrt{3x^2}-8}-frac{sqrt{3x}}{3x+2sqrt{3x}+4}right).left(frac{1+3sqrt{3x^2}}{1+sqrt{3x}}-sqrt{3x}right)a) Tìm ĐKXĐ và rút gọn biểu thức Pb) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyênBài 3: Cho biểu thứcAfrac{sqrt{x+4sqrt{x-4}}+sqrt{x-4sqrt{x-4}}}{sqrt{1-frac{8}{x}+frac{16}{x^2}}}a) Tìm ĐKXĐ và rút gọn biểu thức Ab) Tìm tất cả các giá trị nguyên của x để biểu thức...
Đọc tiếp
Bài 1: Giải phương trình sau:
\(2x^2+5+2\sqrt{x^2+x-2}=5\sqrt{x-1}+5\sqrt{x+2}\)
Bài 2: Cho biểu thức
\(P=\left(\frac{6x+4}{3\sqrt{3x^2}-8}-\frac{\sqrt{3x}}{3x+2\sqrt{3x}+4}\right).\left(\frac{1+3\sqrt{3x^2}}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
a) Tìm ĐKXĐ và rút gọn biểu thức P
b) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyên
Bài 3: Cho biểu thức
\(A=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\)
a) Tìm ĐKXĐ và rút gọn biểu thức A
b) Tìm tất cả các giá trị nguyên của x để biểu thức A có giá trị nguyên
cho biểu thức
A =(\(\frac{x^2+3x}{x^3+3x^2+9x+27}\)+\(\frac{3}{x^2+9}\)) :( \(\frac{1}{x-3}\)- \(\frac{6x}{x^3-3x^2+9x-27}\))
a, rút gọn phân thức P
b, với x>0 thì P không thỏa mãn những giá trị nào
c, tìm giá trị nguyên của x để P có giá trị nguyên
Không chép lại đề nhé:
\(1A=\left(\frac{x\left(x+3\right)}{\left(x+3\right)\left(x^2+9\right)}+\frac{3}{x^2+9}\right):\left(\frac{1}{x-3}-\frac{6x}{\left(x-3\right)\left(x^2+9\right)}\right)\)
\(=\frac{x+3}{x^2+9}:\frac{x^2+9-6x}{\left(x-3\right)\left(x^2+9\right)}\)
\(=\frac{x+3}{x^2+9}.\frac{\left(x-3\right)\left(x^2+9\right)}{\left(x-3\right)^2}\)
\(=\frac{x+3}{x-3}\)
Đúng 0
Bình luận (0)
b/ Với x > 0 thì P không xác định khi x = 3 (vì mẫu sẽ = 0)
c/ \(A=\frac{x+3}{x-3}=1+\frac{6}{x-3}\)
Để A nguyên thì (x - 3) phải là ước nguyên của 6 hay
(x - 3) \(\in\)(- 1; - 2; - 3, - 6; 1; 2; 3; 6)
Thế vào sẽ tìm được A
ĐKXĐ thì b tự làm nhé
Đúng 0
Bình luận (0)


















